Rod calculus

Rod calculus or rod calculation was the mechanical method of algorithmic computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were increasingly replaced by the more convenient and faster abacus. Rod calculus played a key role in the development of Chinese mathematics to its height in the Song dynasty and Yuan dynasty, culminating in the invention of polynomial equations of up to four unknowns in the work of Zhu Shijie.

Japanese counting board with grids

Rod calculus facsimile from the Yongle encyclopedia

Hardware

The basic equipment for carrying out rod calculus is a bundle of counting rods and a counting board. The counting rods are usually made of bamboo sticks, about 12 cm- 15 cm in length, 2mm to 4 mm diameter, sometimes from animal bones, or ivory and jade (for well-heeled merchants). A counting board could be a table top, a wooden board with or without grid, on the floor or on sand.

In 1971 Chinese archaeologists unearthed a bundle of well-preserved animal bone counting rods stored in a silk pouch from a tomb in Qian Yang county in Shanxi province, dated back to the first half of Han dynasty (206 BC – 8AD).^[citation needed] In 1975 a bundle of bamboo counting rods was unearthed.^[citation needed]

The use of counting rods for rod calculus flourished in the Warring States, although no archaeological artefacts were found earlier than the Western Han dynasty (the first half of Han dynasty; however, archaeologists did unearth software artefacts of rod calculus dated back to the Warring States); since the rod calculus software must have gone along with rod calculus hardware, there is no doubt that rod calculus was already flourishing during the Warring States more than 2,200 years ago.

Software

The key software required for rod calculus was a simple 45 phrase positional decimal multiplication table used in China since antiquity, called the nine-nine table, which were learned by heart by pupils, merchants, government officials and mathematicians alike.

Rod numerals

Displaying numbers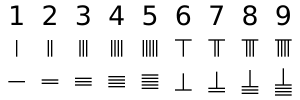

Two forms of Chinese rod numerals

Representation of the number 231 and possible misleading rod placements.

Rod numerals is the only numeric system that uses different placement combination of a single symbol to convey any number or fraction in the Decimal System. For numbers in the units place, every vertical rod represent 1. Two vertical rods represent 2, and so on, until 5 vertical rods, which represents 5. For number between 6 and 9, a biquinary system is used, in which a horizontal bar on top of the vertical bars represent 5. The first row are the number 1 to 9 in rod numerals, and the second row is the same numbers in horizontal form.

For numbers larger than 9, a decimal system is used. Rods placed one place to the left of the units place represent 10 times that number. For the hundreds place, another set of rods is placed to the left which represents 100 times of that number, and so on. As shown in the adjacent image, the number 231 is represented in rod numerals in the top row, with one rod in the units place representing 1, three rods in the tens place representing 30, and two rods in the hundreds place representing 200, with a sum of 231.

When doing calculation, usually there was no grid on the surface. If rod numerals two, three, and one is placed consecutively in the vertical form, there's a possibility of it being mistaken for 51 or 24, as shown in the second and third row of the adjacent image. To avoid confusion, number in consecutive places are placed in alternating vertical and horizontal form, with the units place in vertical form,[1] as shown in the bottom row on the right.

Displaying zeroes

In Rod numerals, zeroes are represented by a space, which serves both as a number and a place holder value. Unlike in Hindu-Arabic numerals, there is no specific symbol to represent zero. Before the introduction of a written zero, in addition to a space to indicate no units, the character in the subsequent unit column would be rotated by 90°, to reduce the ambiguity of a single zero.[2] For example 107 (𝍠 𝍧) and 17 (𝍩𝍧) would be distinguished by rotation, in addition to the space, though multiple zero units could lead to ambiguity, e.g. 1007 (𝍩 𝍧), and 10007 (𝍠 𝍧). In the adjacent image, the number zero is merely represented with a space.

Negative and positive numbers

Song mathematicians used red to represent positive numbers and black for negative numbers. However, another way is to add a slash to the last place to show that the number is negative.[3]

Decimal fraction

The Mathematical Treatise of Sunzi used decimal fraction metrology. The unit of length was 1 chi,

1 chi = 10 cun, 1 cun = 10 fen, 1 fen = 10 li, 1 li = 10 hao, 10 hao = 1 shi, 1 shi = 10 hu.

1 chi 2 cun 3 fen 4 li 5 hao 6 shi 7 hu is laid out on counting board as

where is the unit measurement chi.

Southern Song dynasty mathematician Qin Jiushao extended the use of decimal fraction beyond metrology. In his book Mathematical Treatise in Nine Sections, he formally expressed 1.1446154 day as

日

He marked the unit with a word “日” (day) underneath it.[4]

Addition

Rod calculus addition 3748+289=4037

Rod calculus works on the principle of addition. Unlike Arabic numerals, digits represented by counting rods have additive properties. The process of addition involves mechanically moving the rods without the need of memorising an addition table. This is the biggest difference with Arabic numerals, as one cannot mechanically put 1 and 2 together to form 3, or 2 and 3 together to form 5.

The adjacent image presents the steps in adding 3748 to 289:

1. Place the augend 3748 in the first row, and the addend 289 in the second.
2. Calculate from LEFT to RIGHT, from the 2 of 289 first.
3. Take away two rods from the bottom add to 7 on top to make 9.
4. Move 2 rods from top to bottom 8, carry one to forward to 9, which becomes zero and carries to 3 to make 4, remove 8 from bottom row.
5. Move one rod from 8 on top row to 9 on bottom to form a carry one to next rank and add one rod to 2 rods on top row to make 3 rods, top row left 7.
6. Result 3748+289=4037

The rods in the augend change throughout the addition, while the rods in the addend at the bottom "disappear".

Subtraction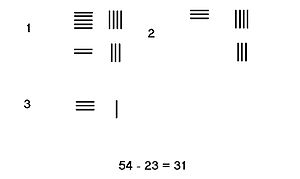

Without borrowing

In situation in which no borrowing is needed, one only needs to take the number of rods in the subtrahend from the minuend. The result of the calculation is the difference. The adjacent image shows the steps in subtracting 23 from 54.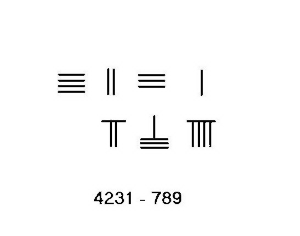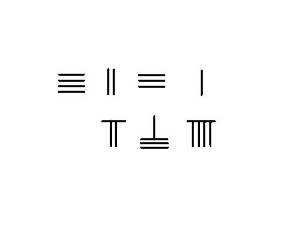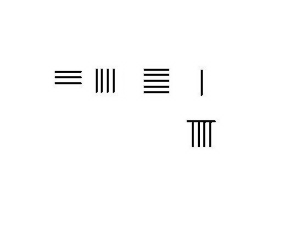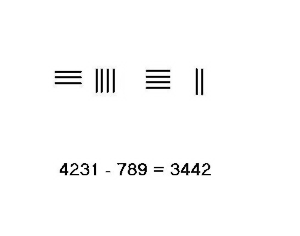

Borrowing

In situations in which borrowing is needed such as 4231–789, one need use a more complicated procedure. The steps for this example are shown on the left.

1. Place the minuend 4231 on top, the subtrahend 789 on the bottom. Calculate from the left to the right.
2. Borrow 1 from the thousands place for a ten in the hundreds place, minus 7 from the row below, the difference 3 is added to the 2 on top to form 5. The 7 on the bottom is subtracted, shown by the space.
3. Borrow 1 from the hundreds place, which leaves 4. The 10 in the tens place minus the 8 below results in 2, which is added to the 3 above to form 5. The top row now is 3451, the bottom 9.
4. Borrow 1 from the 5 in the tens place on top, which leaves 4. The 1 borrowed from the tens is 10 in the units place, subtracting 9 which results in 1, which are added to the top to form 2. With all rods in the bottom row subtracted, the 3442 in the top row is then, the result of the calculation

Multiplication

38x76=2888

al Uqlidis (952 AD)multiplication, a variation of Sunzi multiplication

Sunzi Suanjing described in detail the algorithm of multiplication. On the left are the steps to calculate 38×76:

1. Place the multiplicand on top, the multiplier on bottom. Line up the units place of the multiplier with the highest place of the multiplicand. Leave room in the middle for recording.
2. Start calculating from the highest place of the multiplicand (in the example, calculate 30×76, and then 8×76). Using the multiplication table 3 times 7 is 21. Place 21 in rods in the middle, with 1 aligned with the tens place of the multiplier (on top of 7). Then, 3 times 6 equals 18, place 18 as it is shown in the image. With the 3 in the multiplicand multiplied totally, take the rods off.
3. Move the multiplier one place to the right. Change 7 to horizontal form, 6 to vertical.
4. 8×7 = 56, place 56 in the second row in the middle, with the units place aligned with the digits multiplied in the multiplier. Take 7 out of the multiplier since it has been multiplied.
5. 8×6 = 48, 4 added to the 6 of the last step makes 10, carry 1 over. Take off 8 of the units place in the multiplicand, and take off 6 in the units place of the multiplier.
6. Sum the 2380 and 508 in the middle, which results in 2888: the product.

Division

10th century al-Uqlidis division

Sunzi division ⁠309/7⁠ = 44⁠1/7⁠

al Khwarizmi division of 825AD was identical to Sunzi division algorithm

11th century Kushyar ibn Labban division, a replica of Sunzi division

The animation on the left shows the steps for calculating ⁠309/7⁠ = 44⁠1/7⁠.

1. Place the dividend, 309, in the middle row and the divisor, 7, in the bottom row. Leave space for the top row.
2. Move the divisor, 7, one place to the left, changing it to horizontal form.
3. Using the Chinese multiplication table and division, 30÷7 equals 4 remainder 2. Place the quotient, 4, in the top row and the remainder, 2, in the middle row.
4. Move the divisor one place to the right, changing it to vertical form. 29÷7 equals 4 remainder 1. Place the quotient, 4, on top, leaving the divisor in place. Place the remainder in the middle row in place of the dividend in this step. The result is the quotient is 44 with a remainder of 1

The Sunzi algorithm for division was transmitted in toto by al Khwarizmi to Islamic country from Indian sources in 825AD. Al Khwarizmi's book was translated into Latin in the 13th century, The Sunzi division algorithm later evolved into Galley division in Europe. The division algorithm in Abu'l-Hasan al-Uqlidisi's 925AD book Kitab al-Fusul fi al-Hisab al-Hindi and in 11th century Kushyar ibn Labban's Principles of Hindu Reckoning were identical to Sunzu's division algorithm.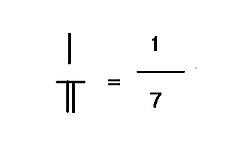

Fractions

If there is a remainder in a place value decimal rod calculus division, both the remainder and the divisor must be left in place with one on top of another. In Liu Hui's notes to Jiuzhang suanshu (2nd century BCE), the number on top is called "shi" (实), while the one at bottom is called "fa" (法). In Sunzi Suanjing, the number on top is called "zi" (子) or "fenzi" (lit., son of fraction), and the one on the bottom is called "mu" (母) or "fenmu" (lit., mother of fraction). Fenzi and Fenmu are also the modern Chinese name for numerator and denominator, respectively. As shown on the right, 1 is the numerator remainder, 7 is the denominator divisor, formed a fraction ⁠1/7⁠. The quotient of the division ⁠309/7⁠ is 44 + ⁠1/7⁠. Liu Hui used a lot of calculations with fractions in Haidao Suanjing.

This form of fraction with numerator on top and denominator at bottom without a horizontal bar in between, was transmitted to Arabic country in an 825AD book by al Khwarizmi via India, and in use by 10th century Abu'l-Hasan al-Uqlidisi and 15th century Jamshīd al-Kāshī's work "Arithematic Key".

Addition

rod calculus fraction addition

⁠1/3⁠ + ⁠2/5⁠

• Put the two numerators 1 and 2 on the left side of counting board, put the two denominators 3 and 5 at the right hand side
• Cross multiply 1 with 5, 2 with 3 to get 5 and 6, replace the numerators with the corresponding cross products.
• Multiply the two denominators 3 × 5 = 15, put at bottom right
• Add the two numerators 5 and 6 = 11 put on top right of counting board.
• Result: ⁠1/3⁠ + ⁠2/5⁠ = ⁠11/15⁠

Subtraction

subtraction of two rod numeral fractions

⁠8/9⁠ − ⁠1/5⁠

• Put down the rod numeral for numerators 1 and 8 at left hand side of a counting board
• Put down the rods for denominators 5 and 9 at the right hand side of a counting board
• Cross multiply 1 × 9 = 9, 5 × 8 = 40, replace the corresponding numerators
• Multiply the denominators 5 × 9 = 45, put 45 at the bottom right of counting board, replace the denominator 5
• Subtract 40 − 9 = 31, put on top right.
• Result: ⁠8/9⁠ − ⁠1/5⁠ = ⁠31/45⁠

Multiplication

rod calculus fraction multiplication

3⁠1/3⁠ × 5⁠2/5⁠

• Arrange the counting rods for 3⁠1/3⁠ and 5⁠2/5⁠ on the counting board as shang, shi, fa tabulation format.
• shang times fa add to shi: 3 × 3 + 1 = 10; 5 × 5 + 2 = 27
• shi multiplied by shi:10 × 27 = 270
• fa multiplied by fa:3 × 5 = 15
• shi divided by fa: 3⁠1/3⁠ × 5⁠2/5⁠ = 18

Highest common factor and fraction reduction

highest common factor

The algorithm for finding the highest common factor of two numbers and reduction of fraction was laid out in Jiuzhang suanshu. The highest common factor is found by successive division with remainders until the last two remainders are identical. The animation on the right illustrates the algorithm for finding the highest common factor of ⁠32,450,625/59,056,400⁠ and reduction of a fraction.

In this case the hcf is 25.

Divide the numerator and denominator by 25. The reduced fraction is ⁠1,298,025/2,362,256⁠.

Interpolation

π in fraction

Calendarist and mathematician He Chengtian (何承天) used fraction interpolation method, called "harmonisation of the divisor of the day" (调日法) to obtain a better approximate value than the old one by iteratively adding the numerators and denominators a "weaker" fraction with a "stronger fraction".[5] Zu Chongzhi's legendary π = ⁠355/113⁠ could be obtained with He Chengtian's method[6]

System of linear equations

system equations

Chapter Eight Rectangular Arrays of Jiuzhang suanshu provided an algorithm for solving System of linear equations by method of elimination:[7]

Problem 8-1: Suppose we have 3 bundles of top quality cereals, 2 bundles of medium quality cereals, and a bundle of low quality cereal with accumulative weight of 39 dou. We also have 2, 3 and 1 bundles of respective cereals amounting to 34 dou; we also have 1,2 and 3 bundles of respective cereals, totaling 26 dou.

Find the quantity of top, medium, and poor quality cereals. In algebra, this problem can be expressed in three system equations with three unknowns.

${\displaystyle {\begin{cases}3x+2y+z=39\\2x+3y+z=34\\x+2y+3z=26\end{cases}}}$

This problem was solved in Jiuzhang suanshu with counting rods laid out on a counting board in a tabular format similar to a 3x4 matrix:

quality	left column	center column	right column
top
medium
low
shi

Algorithm:

1. Multiply the center column with right column top quality number.
2. Repeatedly subtract right column from center column, until the top number of center column=0.
3. multiply the left column with the value of top row of right column.
4. Repeatedly subtract right column from left column, until the top number of left column=0.
5. After applying above elimination algorithm to the reduced center column and left column, the matrix was reduced to triangular shape.

quality	left column	center column	right column
top
medium
low
shi

The amount of one bundle of low quality cereal ${\displaystyle ={\frac {99}{36}}=2{\frac {3}{4}}}$

From which the amount of one bundle of top and medium quality cereals can be found easily:

• One bundle of top quality cereals=9 dou ${\displaystyle {\frac {1}{4}}}$
• One bundle of medium cereal=4 dou ${\displaystyle {\frac {1}{4}}}$

Extraction of Square root

Algorithm for extraction of square root was described in Jiuzhang suanshu and with minor difference in terminology in Sunzi Suanjing.

extraction of square root of 234567 in Sunzi Suanjing

extraction of sq root by Kushyar ibn Labban

The animation shows the algorithm for rod calculus extraction of an approximation of the square root ${\displaystyle {\sqrt {234567}}\approx 484{\tfrac {311}{968}}}$ from the algorithm in chap 2 problem 19 of Sunzi Suanjing:

Now there is a square area 234567, find one side of the square.[8]

The algorithm is as follows:

• Set up 234567 on the counting board, on the second row from top, named shi
• Set up a marker 1 at 10000 position at the 4th row named xia fa
• Estimate the first digit of square root to be counting rod numeral 4, put on the top row (shang) hundreds position,
• Multiply the shang 4 with xiafa 1, put the product 4 on 3rd row named fang fa
• Multiply shang with fang fa deduct the product 4x4=16 from shi: 23-16=7, remain numeral 7.
• double up the fang fa 4 to become 8, shift one position right, and change the vertical 8 into horizontal 8 after moved right.
• Move xia fa two position right.
• Estimate second digit of shang as 8: put numeral 8 at tenth position on top row.
• Multiply xia fa with the new digit of shang, add to fang fa

.

• 8 calls 8 =64, subtract 64 from top row numeral "74", leaving one rod at the most significant digit.
• double the last digit of fang fa 8, add to 80 =96
• Move fang fa96 one position right, change convention;move xia fa "1" two position right.
• Estimate 3rd digit of shang to be 4.
• Multiply new digit of shang 4 with xia fa 1, combined with fang fa to make 964.
• subtract successively 4*9=36,4*6=24,4*4=16 from the shi, leaving 311
• double the last digit 4 of fang fa into 8 and merge with fang fa
• result ${\displaystyle {\sqrt {234567}}\approx 484{\tfrac {311}{968}}}$

North Song dynasty mathematician Jia Xian developed an additive multiplicative algorithm for square root extraction, in which he replaced the traditional "doubling" of "fang fa" by adding shang digit to fang fa digit, with same effect.

Extraction of cubic root

Jia Xian's additive multiplicative method of cubic root extraction

Jiuzhang suanshu vol iv "shaoguang" provided algorithm for extraction of cubic root.

〔一九〕今有積一百八十六萬八百六十七尺。問為立方幾何？答曰：一百二十三尺。

problem 19: We have a 1860867 cubic chi, what is the length of a side ? Answer:123 chi.

${\displaystyle {\sqrt[{3}]{1860867}}=123}$

North Song dynasty mathematician Jia Xian invented a method similar to simplified form of Horner scheme for extraction of cubic root. The animation at right shows Jia Xian's algorithm for solving problem 19 in Jiuzhang suanshu vol 4.

Polynomial equation

Qin Jiushao's "Horner" algorithm

North Song dynasty mathematician Jia Xian invented Horner scheme for solving simple 4th order equation of the form

${\displaystyle x^{4}=a}$

South Song dynasty mathematician Qin Jiushao improved Jia Xian's Horner method to solve polynomial equation up to 10th order. The following is algorithm for solving

${\displaystyle -x^{4}+15245x^{2}-6262506.25=0}$ in his Mathematical Treatise in Nine Sections vol 6 problem 2.[9]

This equation was arranged bottom up with counting rods on counting board in tabular form

0	shang	root
626250625	shi	constant
0	fang	coefficient of x
15245	shang lian	positive coef of ⁠${\displaystyle x^{2}}$⁠
0	fu lian	negative coef of ⁠${\displaystyle x^{2}}$⁠
0	xia lian	coef of ⁠${\displaystyle x^{3}}$⁠
1	yi yu	negative coef of ⁠${\displaystyle x^{4}}$⁠

Algorithm:

1. Arrange the coefficients in tabular form, constant at shi, coeffienct of x at shang lian, the coeffiecnt of ⁠${\displaystyle x^{4}}$⁠ at yi yu;align the numbers at unit rank.
2. Advance shang lian two ranks
3. Advance yi yu three ranks
4. Estimate shang=20
5. let xia lian =shang * yi yu
6. let fu lian=shang *yi yu
7. merge fu lian with shang lian
8. let fang=shang * shang lian
9. subtract shang*fang from shi
10. add shang * yi yu to xia lian
11. retract xia lian 3 ranks, retract yi yu 4 ranks
12. The second digit of shang is 0
13. merge shang lian into fang
14. merge yi yu into xia lian
15. Add yi yu to fu lian, subtract the result from fang, let the result be denominator
16. find the highest common factor =25 and simplify the fraction ${\displaystyle {\frac {32450625}{59056400}}}$
17. solution ${\displaystyle x=20{\frac {1298205}{2362256}}}$

Tian Yuan shu

Tian yuan shu in Li Zhi:Yigu yanduan

Yuan dynasty mathematician Li Zhi developed rod calculus into Tian yuan shu

Example Li Zhi Ceyuan haijing vol II, problem 14 equation of one unknown:

${\displaystyle -x^{2}-680x+96000=0}$

元

Polynomial equations of four unknowns

facsimile of Zhu Shijie: Jade Mirror of Four Unknowns

Mathematician Zhu Shijie further developed rod calculus to include polynomial equations of 2 to four unknowns.

For example, polynomials of three unknowns:

Equation 1:${\displaystyle -y-z-y^{2}*x-x+xyz=0}$

太

Equation 2:${\displaystyle -y-z+x-x^{2}+xz=0}$

Equation 3:${\displaystyle y^{2}-z^{2}+x^{2}=0;}$

太

After successive elimination of two unknowns, the polynomial equations of three unknowns was reduced to a polynomial equation of one unknown:

${\displaystyle x^{4}-6x^{3}+4x^{2}+6x-5=0}$

Solved x=5;

Which ignores 3 other answers, 2 are repeated.

See also

• Chinese mathematics
• Counting rods

References

1. Ronan and Needham, The Shorter Science and Civilisation in China, vol 2, Chapter 1, Mathematics
2. "Chinese numerals". Maths History. Retrieved 2024-04-28.
3. *Ho Peng Yoke， Li， Qi and Shu ISBN 0-486-41445-0
4. Lam Lay Yong, p87-88
5. Jean claude Martzloff, A History of Chinese Mathematics p281
6. Wu Wenjun ed Grand Series of History of Chinese Mathematics vol 4 p125
7. Jean-Claude Martzloff, A History of Chinese Mathematics, p249-257
8. Lay Lay Yong, Ang Tian Se, Fleeting Footsteps, p66-73
9. Jean Claude Martzloff, A History of Chinese Mathematics, p233-246

• Lam Lay Yong (蓝丽蓉) Ang Tian Se (洪天赐), Fleeting Footsteps, World Scientific ISBN 981-02-3696-4
• Jean Claude Martzloff, A History of Chinese Mathematics ISBN 978-3-540-33782-9