Robertson graph

Robertson graph
The Robertson graph is Hamiltonian.
Named after	Neil Robertson
Vertices	19
Edges	38
Radius	3
Diameter	3
Girth	5
Automorphisms	24 (D12)
Chromatic number	3
Chromatic index	5[1]
Book thickness	3
Queue number	2
Properties	Cage Hamiltonian
Table of graphs and parameters

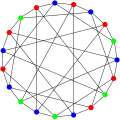
In the mathematical field of graph theory, the Robertson graph or (4,5)-cage, is a 4-regular undirected graph with 19 vertices and 38 edges named after Neil Robertson.[2][3]

The Robertson graph is the unique (4,5)-cage graph and was discovered by Robertson in 1964.[4] As a cage graph, it is the smallest 4-regular graph with girth 5.

It has chromatic number 3, chromatic index 5, diameter 3, radius 3 and is both 4-vertex-connected and 4-edge-connected. It has book thickness 3 and queue number 2.[5]

The Robertson graph is also a Hamiltonian graph which possesses 5,376 distinct directed Hamiltonian cycles.

The Robertson graph is one of the smallest graphs with cop number 4.[6]

Algebraic properties

The Robertson graph is not a vertex-transitive graph and its full automorphism group is isomorphic to the dihedral group of order 24, the group of symmetries of a regular dodecagon, including both rotations and reflections.[7]

The characteristic polynomial of the Robertson graph is

${\displaystyle (x-4)(x-1)^{2}(x^{2}-3)^{2}(x^{2}+x-5)}$

${\displaystyle (x^{2}+x-4)^{2}(x^{2}+x-3)^{2}(x^{2}+x-1).\ }$

Gallery

• 
  The Robertson graph as drawn in the original publication.
• 
  The chromatic number of the Robertson graph is 3.
• 
  The chromatic index of the Robertson graph is 5.

References

1. Weisstein, Eric W. "Class 2 Graph". MathWorld.
2. Weisstein, Eric W. "Robertson Graph". MathWorld.
3. Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications. New York: North Holland, p. 237, 1976.
4. Robertson, N. "The Smallest Graph of Girth 5 and Valency 4." Bull. Amer. Math. Soc. 70, 824-825, 1964.
5. Jessica Wolz, Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
6. Turcotte, J., & Yvon, S. (2021). 4-cop-win graphs have at least 19 vertices. Discrete Applied Mathematics, 301, 74-98.
7. Geoffrey Exoo & Robert Jajcay, Dynamic cage survey, Electr. J. Combin. 15, 2008.