|
Miwin's dice
Miwin's Dice are a set of nontransitive dice invented in 1975 by the physicist Michael Winkelmann. They consist of three different dice with faces bearing numbers from one to nine; opposite faces sum to nine, ten or eleven. The numbers on each die give the sum of 30 and have an arithmetic mean of five. Description Miwin's dice have six sides, each of which bear a number, depicted in a pattern of dots. The standard set is made of wood; special designs are made of titanium or other materials (gold, silver). First set of Miwin's dice: III, IV, V Each die is named for the sum of its two lowest numbers. The dots on each die are colored blue, red or black. Each die has the following numbers:
Numbers 1 and 9, 2 and 7, and 3 and 8 are on opposite sides on all three dice. Additional numbers are 5 and 6 on die III, 4 and 5 on die IV, and 4 and 6 on die V. The dice are designed in such a way that, for every die, another will usually win against it. The probability that a given die in the sequence (III, IV, V, III) will roll a higher number than the next in the sequence is 17/36; a lower number, 16/36. Thus, die III tends to win against IV, IV against V, and V against III. Such dice are known as nontransitive. Second set of Miwin's dice: IX, X, XI Each die is named for the sum of its lowest and highest numbers. The dots on each die are colored yellow, white or green. Each die has the following numbers:
The probability that a given die in the sequence (XI, X, IX, XI) will roll a higher number than the next in the sequence is 17/36; a lower number, 16/36. Thus, die XI tends to win against X, X against IX, and IX against XI. Third and fourth set of Miwin's diceThird set:
fourth set:
The probability that a given die in the first sequence (5, 3, 1, 5) or the second sequence (6, 4, 2, 6) will roll a higher number than the next in the sequence is 5/9; a lower number, 4/9. Mathematical attributesThe dice in the first and second Miwin sets have similar attributes: each die bears each of its numbers exactly once, the sum of the numbers is 30, and each number from one to nine is spread twice over the three dice. This attribute characterizes the implementation of intransitive dice, enabling the different game variants. All the games need only three dice, in comparison to other theoretical nontransitive dice, designed in view of mathematics, such as Efron's dice.[1] Probabilities
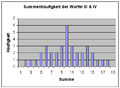
The probability for a given number with all three dice is 11/36, for a given rolled double is 1/36, for any rolled double 1/4. The probability to obtain a rolled double is only 50% compared to normal dice. Cumulative frequency
Reversed intransitivityRemoving the common dots of Miwin's Dice reverses intransitivity.[citation needed]
III:IV = 17:16, III':IV' = 4:5 → IV' > III' analog: III/V, IV/V Equal distribution of random numbersMiwin's dice facilitate generating numbers at random, within a given range, such that each included number is equally-likely to occur. In order to obtain a range that does not begin with 1 or 0, simply add a constant value to bring it into that range (to obtain random numbers between 8 and 16, inclusive, follow the 1 – 9 instructions below, and add seven to the result of each roll).
Other distributions0 – 90 (throw 3 times)Governing probability: P(0) = P(1) = ... = P(90) = 8/9³ = 8/729 To obtain an equal distribution with numbers from 0 – 90, all three dice are rolled, one at a time, in a random order. The result is calculated based on the following rules:
Sample:
This gives 91 numbers, from 0 – 90 with the probability of 8 / 9³, 8 × 91 = 728 = 9³ − 1 0 – 103 (throw 3 times)Governing probability: P(0) = P(1) = ... = P(103) = 7/9³ = 7/729 This gives 104 numbers from 0 – 103 with the probability of 7 / 9³, 7 × 104 = 728 = 9³ − 1 0 – 728 (throw 3 times)Governing probability: P(0) = P(1) = ... = P(728) = 1 / 9³ = 1 / 729 This gives 729 numbers, from 0 – 728, with the probability of 1 / 9³. One die is rolled at a time, taken at random. Create a number system of base 9:
This system yields this maximum: 8 × 9² + 8 × 9 + 8 × 9° = 648 + 72 + 8 = 728 = 9³ − 1 Examples:
Combinations with Miwin's dice type III, IV, and V
3 throws, random selection of one of the dice for each throw, type is used as attribute:
5832 = 2 × 2 × 2 × 9 × 9 × 9 = 18³ numbers are possible. GamesSince the middle of the 1980s, the press wrote about the games.[2] Winkelmann presented games himself, for example, in 1987 in Vienna, at the "Österrechischen Spielefest, Stiftung Spielen in Österreich", Leopoldsdorf, where "Miwin's dice" won the prize "Novel Independent Dice Game of the Year". In 1989, the games were reviewed by the periodical "Die Spielwiese".[3] At that time, 14 alternatives of gambling and strategic games existed for Miwin's dice. The periodical "Spielbox" had two variants of games for Miwin's dice in the category "Unser Spiel im Heft" (now known as "Edition Spielbox"): the solitaire game 5 to 4, and the two-player strategic game Bitis. In 1994, Vienna's Arquus publishing house published Winkelmann's book Göttliche Spiele,[4] which contained 92 games, a master copy for four game boards, documentation about the mathematical attributes of the dice and a set of Miwin's dice. There are even more game variants listed on Winkelmann's website.[5] Solitaire games and games for up to nine players have been developed. Games are appropriate for players over six years of age. Some games require a game board; playing time varies from 5 to 60 minutes. Variants 0 – 801st variantTwo dice are rolled, chosen at random, one at a time. Each pair is scored by multiplying the first by nine and subtracting the second from the result: 1st throw × 9 − 2nd throw. Examples:
This variant provides numbers from 0 – 80 with a probability of 1 / 9² = 1 / 81. 2nd variantTwo dice are rolled, chosen at random, one at a time. The pair is scored according to the following rules:
This variant provides numbers from 0 – 80 with a probability of 1 / 9² = 1 / 81. 3rd variantTwo dice are rolled, chosen at random, one at a time. The score is obtained according to the following rules:
Examples:
Notes
External links
Published games
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||