|
Ground-based interferometric gravitational-wave searchGround-based interferometric gravitational-wave search refers to the use of extremely large interferometers built on the ground to passively detect (or "observe") gravitational wave events from throughout the cosmos.[1] Most recorded gravitational wave observations have been made using this technique; the first detection, revealing the merger of two black holes, was made in 2015 by the LIGO sites. As of 2024[update], major detectors are the two LIGO sites in the United States, Virgo in Italy and KAGRA in Japan, which are all part of the second generation of operational detectors. Developing projects include LIGO-India as part of the second generation, and the Einstein Telescope and Cosmic Explorer forming a third generation. Space-borne interferometers such as LISA are also planned, with a similar concept but targeting different kind of sources and using very different technologies.[1]: 40 HistoryWhile gravitational waves were first formulated as part of general relativity by Einstein in 1916,[2] there were no real attempts to detect them until the 1960s, when Joseph Weber created the first of so-called "Weber bars". While these proved unable to reach the required sensitivity for detecting gravitational waves, many research groups focused on this topic were created at that time. While a lot of efforts were dedicated to improving the resonant bar design, the idea of using a large interferometer for gravitational wave detection was formulated in the 1970s and began to gain traction in the 1980s, leading to the foundation of LIGO in 1984 and Virgo in 1989.[3][4] Most of the current large interferometers started construction in the 1990s and finished in the early 2000s (1999 for LIGO,[5] 2003 for Virgo,[6] 2002 for GEO 600). After a few years of observation and improvements to reach their target sensitivity, it became clear that a detection was unlikely and that further upgrades were required, leading to large projects now labelled as the "second generation of detectors" (Advanced LIGO and Virgo), with important sensitivity gains. This periods also marked the beginning of joint observing periods between the different detectors, which are crucial to confirm the validity of a signal, and sparked collaborations between the different teams. The second generation upgrades were made during the early 2010s, lasting from 2010 to 2014 for LIGO and 2011 to 2017 for Virgo. In parallel, the KAGRA project was launched in Japan in 2010. In 2015, soon after restarting observations, the two LIGO detectors achieved the first direct observation of gravitational waves. This marked the beginning of the still ongoing series of gravitational wave observation periods, labelled O1 through O5;[7] Virgo joined the observations in 2017, near the end of the O2 period, leading quickly to the first three-detector observation, and a few days later the GW170817 event, which is the only one to date to have been observed both with gravitational waves and electromagnetic radiation. KAGRA was completed in 2020, only observing for brief periods of time due to its low sensitivity up until now. The O4 observing run is currently ongoing, and expected to last until June 2025. More than 90 confirmed detections have been published; the collaborations now also produce live alerts when signals are detected, with more than 100 significant alerts already emitted during O4.[8] PrincipleIn general relativity, a gravitational wave is a space-time perturbation which propagates at the speed of light. It thus slightly curves space-time, which locally changes the light path. Mathematically speaking, if is the amplitude (assumed to be small) of the incoming gravitational wave and the length of the optical cavity in which the light is in circulation, the change of the optical path due to the gravitational wave is given by the formula:[9]with being a geometrical factor which depends on the relative orientation between the cavity and the direction of propagation of the incoming gravitational wave. In other terms, the change in length is proportional to both to the length of the cavity and the amplitude of the gravitational wave. InterferometerIn a typical configuration, the detector is a Michelson interferometer whose mirrors are suspended. A laser is divided into two beams by a beam splitter tilted by 45 degrees. The two beams propagate in the two perpendicular arms of the interferometer, are reflected by mirrors located at the end of the arms, and recombine on the beam splitter, generating interferences which are detected by a photodiode. An incoming gravitational wave changes the optical path of the laser beams in the arms, which then changes the interference pattern recorded by the photodiode. This means the various mirrors of the interferometer must be "frozen" in position: when they move, the optical cavity length changes and so does the interference signal read at the instrument output port. The mirror positions relative to a reference and their alignment are monitored accurately in real time[10] with a precision better than the tenth of a nanometre for the lengths;[11] at the level of a few nano radians for the angles. The more sensitive the detector, the narrower its optimal working point. Reaching that working point from an initial configuration in which the various mirrors are moving freely is a control system challenge; a complex series of steps is required to coordinate all the steerable parts of the interferometer. Once the working point is achieved, corrections are continuously applied to keep it in the optimal configuration.[12] The signal induced by a potential gravitational wave is thus "embedded" in the light intensity variations detected at the interferometer output.[13] Yet, several external causes—globally denoted as noise—change the interference pattern perpetually and significantly. Should nothing be done to remove or mitigate them, the expected physical signals would be buried in noise and would then remain undetectable. The design of detectors like Virgo and LIGO thus requires a detailed inventory of all noise sources which could impact the measurement, allowing a strong and continuing effort to reduce them as much as possible.[14][11] Using an interferometer rather than a single optical cavity allows one to significantly enhance the detector's sensitivity to gravitational waves. Indeed, in this configuration based on an interference measurement, the contributions from some experimental noises are strongly reduced: instead of being proportional to the length of the single cavity, they depend in that case on the length difference between the arms (so equal arm length cancels the noise). In addition, the interferometer configuration benefits from the differential effect induced by a gravitational wave in the plane transverse to its direction of propagation: when the length of an optical path changes by a quantity , the perpendicular optical path of the same length changes by (same magnitude but opposite sign). And the interference at the output port of a Michelson interferometer depends on the difference of length between the two arms: the measured effect is hence amplified by a factor of 2 compared to a simple cavity. The optimal working point of an interferometric detector of gravitational waves is slightly detuned from the "dark fringe", a configuration in which the two laser beams recombined on the beam splitter interfere in a destructive way: almost no light is detected at the output port. DetectorsLIGO LIGO is composed of two different detectors, one in Hanford, Washington and one in Livingston, Louisiana (they are thus separated by around 3000 km); the two detectors have very similar design, with 4 km long arms, although there are minor differences between the two. They were part of the first generation of detectors, and were completed in 2002; in 2010, they were shut down for an important set of upgrades, termed "Advanced LIGO", making the improved detector a part of the second generation. These upgrades were finished in early 2015, following which the two detectors made the first detection of gravitational waves. Virgo Virgo is a single detector located near Pisa, Italy, with 3 km long arms. It was part of the first generation of detectors, following its completion in 2003; it was shut down in 2011 to prepare for the "Advanced Virgo" second-generation upgrades. The upgrades were completed in 2017, allowing it to join the "O2" run, quickly making the first three-detector detection jointly with LIGO. KAGRA KAGRA (formerly known as LCGT) is a single interferometer with 3 km long arms, based in the Kamioka Observatory in Japan, which is part of the second generation of detectors. It was first made operational in 2020, although it has not been able to make a detection yet. Although the base design is similar to LIGO and Virgo, it is built underground and integrates cryogenic mirrors, which is why it has often been referred to as a "2.5 generation detector".[15] Other detectorsGEO600 was initially designed as a British-German effort to build an interferometer with 3 km long arms; it was later downscaled to 600 m due to funding reasons. It was completed in 2002 and is located near Hanover, Germany. Although it has limited capacities (especially in the lower frequency range), making a detection unlikely, it plays a key role in the gravitational wave network as a testbed for many new technologies.[16] TAMA 300 (and its predecessor, the prototype TAMA 20) was a Japanese detector with 300 m arms, built at the Mitaka university. It was partly designed as a stepstone for larger detectors (including KAGRA), and operated between 1999 and 2004. It has now been repurposed as a testbed for new technologies.[17] The CLIO detector, with 100 m arms and located in the Kamioka mine, is another test detector, specifically designed to test the cryogenic technology used in KAGRA.[18] LIGO-Australia is a defunct project which was envisioned to be built on the model of the LIGO detector in Australia, but was finally not funded by the Australian government; the project was later relocated to become LIGO-India. The Fermilab Holometer, with its 39 m long arms, probes a pretty different range in frequency than other interferometers, aiming for the MHz range. Future detectorsLIGO-IndiaLIGO-India is a current project of a single interferometer based in Aundha, India, following a design very similar to LIGO (with support from the LIGO collaboration). It has received approval from the Indian government in 2023, and is planned to be completed around 2030.[19] Cosmic ExplorerCosmic Explorer is a project for a third-generation detector, featuring two interferometers with respectively 40 km and 20 km long arms located in two different places in the United States. It relies on a design similar to LIGO, leveraging the experience from the two LIGO detectors, scaled to the much longer arm length. It is currently going through the process of approval by the NSF. If approved, it should be completed by the end of the 2030s.[20] Einstein TelescopeEinstein Telescope is a European project for a third-generation detector; it is currently planned to use a design with three 10 km arms arranged in an equilateral triangle (effectively acting as 3 interferometers), which would be built underground; it would also use cryogenic mirrors. It is currently planned to be completed around 2035, with construction starting in 2026.  Science case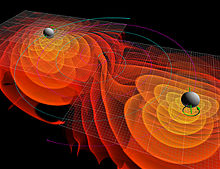 Ground-based detectors are designed to study gravitational waves from astrophysical sources. By design, they can only detect waves with a frequency ranging from a few Hz to a few thousand of Hz. The main known gravitational-wave emitting systems within this range are: black hole and/or neutron star binary mergers, rotating neutron stars, bursts and supernovae explosions, and even the gravitational wave background generated in the instants following the Big Bang. Moreover, gravitational radiation may also lead to the discovery of unexpected and theoretically predicted exotic objects. Transient sources Coalescences of black holes and neutron starsWhen two massive and compact objects such as black holes and neutron stars orbit each other in a binary system, they emit gravitational radiation and, therefore, lose energy. Hence, they begin to get closer to each other, increasing the frequency and the amplitude of the gravitational waves; this first phase of the coalescence phenomenon, called the "inspiral", can last for millions of years. This culminates in the merger of the two objects, eventually forming a single compact object (generally a black hole). The part of the waveform corresponding to the merger has the largest amplitude and highest frequency, and can only be modeled by performing numerical relativity simulations of these systems. In the case of black holes, a signal is still emitted during a few seconds after the merger, while the new black hole "settles in"; this signal is known as the "ringdown". Current detectors are only sensitive to the late stages of the coalescence of black hole and neutron star binaries: only the last seconds of the whole process can currently be observed (including the end of the inspiral phase, the merger itself and part of the ringdown). The typical shape of the detectable signal is known as the "chirp", as it resembles the sound emitted by some birds, with a rapid increase in amplitude and frequency. All the gravitational waves signal detected so far originate from black hole or neutron star mergers.[21][22] Bursts Any signal lasting from a few milliseconds to a few seconds is considered a gravitational wave burst. Supernova explosions—the gravitational collapse of massive stars at the end of their lives—emit gravitational radiation that may be seen by current interferometers.[23] A multi-messenger detection (electromagnetic and gravitational radiation, and neutrinos) would help to better understand the supernova process and the formation of black holes.[24] Other possible burst candidates include perturbations in neutron stars,[25] black hole encounters,[26] "memory" effects arising from the non-linearity of general relativity[27] or cosmic strings.[28] Some phenomena may also generate "long" bursts (longer than 1 second), like instabilities in a black hole accretion disk, or in newly formed black holes and neutron stars when some of the matter ejected during the supernova falls back towards the compact object.[29] Continuous sourcesThe main expected sources of continuous gravitational waves are neutron stars, very compact objects resulting from the collapse of massive stars. In particular, pulsars are special cases of neutron stars that emit light pulses periodically: they can spin up to hundreds of times per second (the fastest spinning pulsar currently known is PSR J1748−2446ad, which spins 716 times per second[30]). Any small deviation from axial symmetry (a tiny "mountain" on the surface) will generate long duration periodic gravitational waves.[31] A number of potential mechanisms have been identified which could generate some "mountains" due to thermal, mechanic, or magnetic effects; accretion may also induce a break in axial symmetry.[32][33][34] Another possible source of continuous waves in the current detection range could be more exotic objects, such as dark matter candidates. Axions rotating around a black hole[32] or binary systems consisting of a primordial low-mass black hole and another compact object have in particular been suggested as potential sources. Some possible types of dark matter may also be detected by the interferometers directly, by interacting with optical elements of the device.[35] Stochastic backgroundSeveral physical phenomena may be the source of a gravitational wave stochastic background, an additional source of noise of astrophysical and/or cosmological origin. It represents a (usually) continuous source of gravitational waves, but unlike other continuous wave sources (like rotating neutron stars), it comes from large regions of the sky instead of a single location.[36] The cosmic microwave background (CMB) is the earliest signal of the Universe that can be observed in the electromagnetic spectrum. However, cosmological models predict the emission of gravitational waves generated instants after the Big Bang. Because gravitational waves interact very weakly with matter, detecting such background would give more insight in the cosmological evolution of our Universe.[37] In particular, it could provide evidence for inflation, from gravitational waves emitted either by the process of inflation itself (according to some theories)[38][39] or at the end of inflation;[40] first-order phase transitions may also produce gravitational waves.[36] Primordial black holes, which may form during the early universe, are also a potential source of a stochastic background for that period.[41] Moreover, current detectors may be able to detect an astrophysical background resulting from the superposition of all faint and distant sources emitting gravitational waves at all times, which would help to study the evolution of astrophysical sources and star formation. The most likely sources to contribute to the astrophysical background are binary neutron stars,[42] binary black holes,[43] or neutron star-black hole binaries. Other possible sources include supernovae and pulsars.[36] It is expected that this type of background will be the first kind to be detected by the current ground interferometers.[44] Finally, cosmic strings may represent a source of gravitational wave background, whose detection could provide proof that cosmic strings actually exist.[45][28] Exotic sourcesNon-conventional, alternative models of compact objects have been proposed by physicists. Some examples of these models can be described within general relativity (quark and strange stars,[46] boson and Proca stars,[47] Kerr black holes with scalar and Proca hair[48]), others arise from some approaches to quantum gravity (cosmic strings,[49] fuzzballs,[50] gravastars[51]), or come from alternative theories of gravity (scalarised neutron stars or black holes, wormholes[52]). Theoretically predicted exotic compact objects could now be detected and would help to elucidate the true nature of gravity or discover new forms of matter. Furthermore, completely unexpected phenomena may be observed, unveiling new physics. Fundamental properties of gravityGravitational wave polarizationGravitational waves are expected to have two "tensor" polarizations, nicknamed "plus" and "cross" due to their effects on a ring of particle (displayed in the figure below). A single gravitational wave is usually a superposition of these two polarizations, depending on the orientation of the source. In addition, some theories of gravity allow for additional polarizations to exist: the two "vector" polarizations (x and y), and the two "scalar" polarizations ("breathing" and "longitudinal"). Detecting these additional polarizations could provide evidence for physics beyond general relativity.[53] The polarizations can only be distinguished using several detectors; they could only be properly probed after Virgo was introduced, as the two LIGO detectors are almost co-aligned.[54] They can be measured from compact binary coalescences,[55][56] but also from the stochastic background[57] and continuous waves.[58] With the combination of the current detectors, it is possible to determine the presence or absence of the additional polarizations, but not their nature; a total of 5 independent detectors would be required to fully separate all the polarizations (except for the longitudinal and breathing polarizations, which cannot be distinguished from each other by current detector designs[56]).[59]
Lensed gravitational wavesGeneral relativity predicts that a gravitational wave should be subject to gravitational lensing, just as light waves are; that is, the trajectory of a gravitational wave will be curved by the presence of a massive object (typically a galaxy or a galaxy cluster) near its path.[60] This can result in an increase in the amplitude of the wave, or even multiple observations of the event at different times, as we currently observe for the light of supernovae. Such events are predicted to be common enough to be detected by the current detectors in the near future.[61] Microlensing effects are also predicted.[62] Detecting a lensed event would allow for a very precise localization, as well as further tests of the speed of gravity and of the polarization.[60] Cosmological measurementsGravitational waves also provide a new way to measure some cosmological parameters, and in particular the Hubble constant , which represents the rate of the expansion of the universe and whose value is currently disputed due to conflicting measurement from different methods. The main benefit of this method is that the source luminosity distance measured from the gravitational wave signal does not rely on other measurements or assumptions, as is usually the case. There are two main possibilities for measuring with gravitational waves in current detectors:
Testing general relativityThe measurement of gravitational wave signals offers a unique perspective for testing results from general relativity, as they are produced in environments where the gravitational field is very strong (e.g., near black holes). Such tests may uncover physics beyond general relativity, or possible issues in the models.[65]
Data analysisThe detection of gravitational waves within the output of the detectors (typically known as the "strain") is a complex process. Currently, most of the data processing is done within the LIGO-Virgo-KAGRA (LVK) collaboration; teams outside of the collaboration also produce results on the data once it is released publicly.[70] The data from the current detectors is initially only available to LVK members; segments of data around detected events are released at the time of publication of the related paper, and the full data is released after a proprietary period, currently lasting 18 months. During the third observing run (O3), this resulted in two separated data releases (O3a and O3b), corresponding to the first six months and last six months of the run respectively.[71] The data is then available for anyone on the Gravitational Wave Open Science Center (GWOSC) platform.[72][73] Transient searchesEvent detection pipelinesThe various software used for the analysis of gravitational wave signals are usually referred to as "search pipelines", as they often encompass many steps of the data processing. During the O3 run, five different pipelines were used to identify event candidates within the data and collect a list of observations of short-lived ("transient") gravitational waves signals in a catalog publication. Four of them (GstLAL, PyCBC, MBTA, and SPIIR) were dedicated to the detection of compact binary coalescences (CBC, the only type of event detected so far), while the fifth one (cWB) was designed to detect any transient signal. All five pipelines have been used during the run ("online") as part of the low-latency alert system, and after the run ("offline") to reassess the significance of the candidates and spot events which may have been missed (except for SPIIR, which was only run online)[74] The oLIB pipeline, also looking for generic "burst" signals, has also been used to generate alerts, but not for the catalogs.[75][76] In addition, two other pipelines have been used specifically for burst searches after the run, as they are too computationally expensive to be run online : BayesWave, a pipeline using Bayesian techniques which was used to further investigate events by cWB,[77] and STAMPS-AS, which is designed to look specifically for long-duration bursts (more than 1 second).[29][78] The four CBC pipelines all rely on the concept of matched filtering, a technique used to search for a known signal within noisy data in an optimal way. This technique requires some knowledge of what the signal looks like, and is thus dependent on the model used to simulate it. Although reasonable models exist, the complexity of the equations governing the dynamics of a compact merger makes the generation of accurate waveforms challenging; the development of new waveforms is still an active field of research.[79][80] In addition, the sources cover a wide range of possible parameters (masses and spins of the two objects, location in the sky) which will yield different waveforms, instead of having one specific signal. This prompts the researchers to generate "template banks" containing a large amount of different waveforms corresponding to different parameters; a compromise has to be done between how tight the bank is (maximizing the number of detections) and the limited computational resources available to carry out the search with all the templates. How to generate such template banks efficiently is also an active field of research.[81] During the search, the matched filtering is performed on every waveform within the (pre-calculated) template bank. Although the four searches use the same technique, they all have different optimizations and specificities on how they handle the data. In particular, they use different techniques for estimating the significance of an event, for discriminating between real events and glitches, and for combining the data from the different detectors; they also use different template banks. The cWB (coherent wave burst) pipeline uses a different approach: it works by grouping the data from the different detectors and carrying a joint analysis to look for coherent signals appearing in several detectors at once. Although its sensitivity for binary mergers is less than the dedicated CBC pipelines, its strength lies in being able to detect signals from any kind of sources, as it does not require any assumption on the shape of the signal (which is why it often referred to as an "unmodeled" search).[82] Low-latencyThe low-latency system is designed to produce alerts for astronomers when gravitational events are detected, with the hope that an electromagnetic counterpart can be observed. This is achieved by centralizing the event candidates from the different analysis pipelines in the gravitational-wave candidate event database (GraceDB),[83] from which the data is processed. If an event is deemed significant enough, a rapid sky localization is produced and preliminary alerts are sent autonomously within the span of a few minutes; after a more precise evaluation of the source parameters, as well as human vetting, a new alert or a retraction notice is sent within a day.[84] The alerts are sent through the GCN, which also centralizes alerts from gamma-ray and neutrino telescopes, as well as SciMMA.[85][86] A total of 78 alerts were sent during the O3 run, of which 23 were later retracted.[74] Parameter estimationAfter an event has been detected by one of the event detection pipelines, a deeper analysis is performed to get a more precise estimation of the parameters of the source and the measurement uncertainty. During the O3 run, this was carried out using several different pipelines, including Bilby and RIFT. These pipelines employ Bayesian methods to quantify the uncertainty, including MCMC and nested sampling.[74] Search for counterpartsWhile many astronomers try to follow-up the low-latency alerts from gravitational wave detectors, the reverse also exists: electromagnetic events expected to have an associated gravitational wave emission are subjected to a deeper search. One of the prime targets for these are gamma-ray bursts; these are thought to be associated with supernovae ("long" bursts, lasting more than 2 seconds) and with compact binary coalescences involving neutron stars ("short" bursts).[87] The merger of two neutron stars in particular has been confirmed to be associated with both a gamma-ray burst and gravitational waves with the GW170817 event.[42] Searches targeted toward gamma-ray bursts observations have been performed on data from the past runs using the pyGRB pipeline[88] for CBC, using methods similar to the regular searches, but centered around the time of the bursts and targeting only the sky area found by gamma-ray observatories. An unmodelled search was also carried out using the X-pipeline package, in a similar fashion as regular unmodelled searches.[89][87] In addition to these searches, several pipelines are looking for coincidences between alerts from gravitational waves and alerts from other detectors. In particular, the RAVEN pipeline is part of the low-latency infrastructure and analyzes the coincidence with gamma-ray burst events and other sources.[90] The LLAMA pipeline is also dedicated to identifying such coincidences with neutrino events, predominantly from IceCube.[91] Continuous wave searchesSearches dedicated to periodic gravitational waves—such as the ones generated by rapidly rotating neutron stars—are generally referred to as continuous wave searches. These can be divided in three categories: all-sky searches, which look for unknown signals from any direction, directed searches, which aim for objects with known positions but unknown frequency, and targeted searches, which hunt for signals from sources where both the position and the frequency are known. The directed and targeted searches are motivated by the fact that all-sky searches are extremely computationally expensive, and thus require trade-offs that limit their sensitivity.[32][34] The principal challenge in continuous wave search is that the signal is much weaker than current detected transients, meaning that one must observe a long time period to accumulate enough data to detect it, as the signal-to-noise ratio scales with the square root of the observing time (intuitively, the signal will add up over the observing duration while the noise will not).[92] The issue is that over such long periods of time, the frequency from the source will evolve, and the motion of the Earth around the Sun will affect the frequency via the Doppler effect. This greatly increases the computational cost of the search, even more so when the frequency is unknown. Although there are mitigation strategies, such as semi-coherent searches, where the analysis is performed separately on segments from the data rather than the full data, these result in a loss of sensitivity.[32] Other approaches include cross-correlation, inspired by stochastic wave searches, which takes advantage of having multiple detectors to look for a correlated signal in a pair of detectors.[93] Stochastic wave searchesThe stochastic gravitational wave background is another target for data analysis teams. By definition, it can be seen as a source of noise in the detectors; the main challenge is to separate it from the other sources of noise, and measure its power spectral density. The easiest method for solving this issue is to look for correlations within a network of several detectors; the idea being that the noise related to the gravitational wave background will be identical in all detectors, while the instrumental noise will (in principle) not be correlated across the detectors. Another possible approach would be to look for excess power not accounted by other noise sources; however, this proves impractical for current interferometers as the noise is not known well enough compared to the expected power of the stochastic background.[94] Only searches based on cross-correlation between detectors are currently in use by the LVK collaboration,[95] although other types of searches are also developed.[96][97] This kind of search must also account for factors such as the detectors antenna pattern, the motion of the Earth, and the distance between the detectors. Assumptions also have to be made on some properties of the background; it is common to assume that it is Gaussian and isotropic, but searches for anisotropic, non-Gaussian, and more exotic backgrounds also exist.[94][96] Gravitational wave properties searchesA number of software have been developed to investigate the physics surrounding gravitational waves. These analyses are generally performed offline (after the run), and often rely on the results from the other searches (currently mostly CBC searches). Several analyses are performed to look for events observed multiple time due to lensing, first by trying to match all the known events together, and then by performing a joint analysis for the most promising pair of events; these analyses have been performed using LALInference and HANABI software. Additional searches for events which may have been missed by the regular CBC searches are also performed, by reusing the existing CBC pipelines.[60] Software designed for estimating the Hubble constant has also been developed. The gwcosmo pipeline performs a Bayesian analysis to determine a distribution of the possible values of the constant, both using "dark sirens" (CBC events without electromagnetic counterpart), which can be correlated with a galaxy catalog, and events with an electromagnetic counterpart for which a direct estimation can be made based on the distance measured with gravitational waves and the identified host galaxy.[98][99] This requires assuming a specific population of black holes, which may be a significant source of bias; recent analyses have been trying to circumvent this issue by fitting both the population and the Hubble constant simultaneously.[100] References
|








