|
G.992.1
In telecommunications, ITU-T G.992.1 (better known as G.dmt) is an ITU standard for ADSL using discrete multitone modulation (DMT). G.dmt full-rate ADSL expands the usable bandwidth of existing copper telephone lines, delivering high-speed data communications at rates up to 8 Mbit/s downstream and 1.3 Mbit/s upstream.[1] DMT allocates from 2 to 15 bits per channel (bin). As line conditions change, bit swapping allows the modem to swap bits around different channels, without retraining, as each channel becomes more or less capable. If bit swapping is disabled then this does not happen and the modem needs to retrain in order to adapt to changing line conditions. There are 2 competing standards for DMT ADSL - ANSI and G.dmt; ANSI T1.413 is a North American standard, G.992.1 (G.dmt) is an ITU (United Nations Telecom committee) standard. G.dmt is used most commonly today, throughout the world, but the ANSI standard was formerly popular in North America. There is a difference in framing between the two, and selecting the wrong standard can cause frame alignment errors every 5 or so minutes. Error correction is done using Reed–Solomon encoding and further protection can be used if Trellis encoding is used at both ends. Interleaving can also increase the robustness of the line but increases latency. DMT history and line rates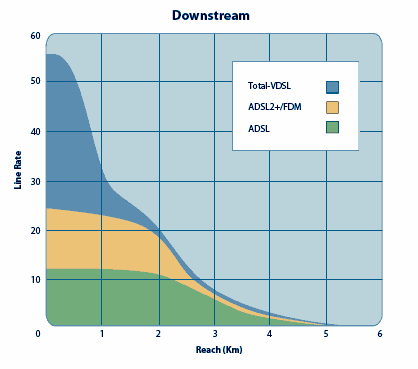  Modulation is the overlaying of information (or the signal) onto an electronic or optical carrier waveform. There are two competing and incompatible standards for modulating the ADSL signal, known as discrete multitone modulation (DMT) and Carrierless Amplitude Phase (CAP). CAP was the original technology used for DSL deployments, but the most widely used method now is DMT. The graphs on the right summarise the speeds obtainable for each ADSL standard based on line length and attenuation. The second graph is of more importance since it is attenuation which is the governing factor for line speed because attenuation rate over distance can vary significantly between various copper lines due to their quality and other factors. ADSL2 is able to extend the reach of extremely long lines that have around 90 dB attenuation. Standard ADSL is only able to provide a service on lines with an attenuation no greater than about 75 dB. DMT technical detailsBins (carrier channels)Discrete Multi-Tone (DMT), the most widely used modulation method, separates the ADSL signal into 255 carriers (bins) centred on multiples of 4.3125 kHz. DMT has 224 downstream frequency bins and up to 31 upstream bins. Bin 0 is at DC and is not used. When voice (POTS) is used on the same line, then bin 7 is the lowest bin used for ADSL. The centre frequency of bin N is (N x 4.3125) kHz. The spectrum of each bin overlaps that of its neighbours: it is not confined to a 4.3125 kHz wide channel. The orthogonality of COFDM makes this possible without interference. Up to 15 bits per symbol can be encoded in a bin on a good quality line. The frequency layout can be summarised as:
Typically, a few bins around 31-32 are not used in order to prevent interference between upstream and downstream bins either side of 138 kHz. These unused bins constitute a guard band to be chosen by each DSLAM manufacturer - it is not defined by the G.992.1 specification. Coded orthogonal frequency-division multiplexing (COFDM)The use of bins produces a transmission system known as coded orthogonal frequency-division multiplexing (COFDM). In the context of G.992.1, the term "Discrete Multi-Tone" (DMT) is used instead, hence the alternative name of the standard, G.dmt. Using DMT is useful since it allows the communications equipment (user modem/router and exchange/DSLAM) to select only bins which are usable on the line thus effectively obtaining the best overall bit rate from the line at any given moment in time. With COFDM, a combined signal containing many frequencies (for each bin) is transmitted down the line. Fast Fourier Transform (and the inverse iFFT) is used to convert the signal on the line into the individual bins. Reducing bit errors with QAM or PSKA type of quadrature amplitude modulation (QAM) or phase-shift keying (PSK) is used to encode the bits within each bin. This is a complex and mathematical subject and will not be discussed further here. However, much research has been done on these modulation techniques and they are used for transmission because they allow the SNR to be improved, thus lowering the noise floor and enabling more reliable transmission of a signal with fewer errors. The gain obtainable above the noise floor can be anything from 0.5 to 1.5 dB and these small amounts make a vast difference when sending signals over long distance copper lines of 6 km or more. Bin quality and bit rateThe quality of the line (how well it performs) at the frequency of the bin in question determines how many bits can be encoded within that bin. As with all transmission lines, it depends on the attenuation and signal-to-noise ratio. SNR may differ for each bin and this plays an important factor for deciding how many bits can be encoded reliably on it. Generally speaking, 1 bit can be encoded reliably for each 3 dB of available dynamic range above the noise floor within a transmission medium so, for example, a bin with an SNR of 18 dB would be able to accommodate 6 bits. Echo cancellationEcho cancellation can be used so the downstream channel overlaps the upstream channel, or vice versa, meaning simultaneous upstream and downstream signals are sent. Echo cancellation is optional and is typically not used. DMT bits-per-bin examplesBelow are examples of how the bin layout may look on various ADSL modems. Both show similar information and in each example there are 256 bins with a varied number of bits being encoded on each one. We can see that at around the frequency range of bin 33, the SNR is 40 dB with the bits per bin being around 6 or 7. Textual-----------------------------------------------------------------------------
Bin SNR Gain Bi - Bin SNR Gain Bi - Bin SNR Gain Bi - Bin SNR Gain Bi
dB dB ts dB dB ts dB dB ts dB dB ts
--- ----- ---- -- - --- ----- ---- -- - --- ----- ---- -- - --- ----- ---- --
0 0.0 0.0 0 * 1 0.0 0.0 0 * 2 0.0 0.0 0 * 3 0.0 0.0 0 <- unused
4 0.0 0.0 0 * 5 0.0 0.0 0 * 6 0.0 0.7 0 * 7 0.0 0.7 0 <- unused
8 0.0 0.9 2 * 9 0.0 1.2 4 * 10 0.0 1.0 5 * 11 0.0 0.8 5 <- upstream [BEGIN]
12 0.0 1.0 6 * 13 0.0 0.9 6 * 14 0.0 0.9 6 * 15 0.0 1.1 7 <- upstream
16 0.0 1.1 7 * 17 0.0 1.0 7 * 18 0.0 0.9 7 * 19 0.0 0.7 7 <- upstream
20 0.0 1.0 6 * 21 0.0 0.9 5 * 22 0.0 0.9 4 * 23 0.0 1.2 4 <- upstream
24 0.0 1.3 3 * 25 0.0 1.0 2 * 26 0.0 0.7 0 * 27 0.0 0.7 0 <- upstream [END]
28 0.0 0.7 0 * 29 0.0 0.0 0 * 30 0.0 0.0 0 * 31 39.9 0.9 6 <- downstream [BEGIN]
32 38.4 0.9 6 * 33 39.9 1.1 7 * 34 256.0 1.0 0 * 35 39.8 1.2 7 <- downstream (1 unused bin - interference?)
36 39.8 1.1 7 * 37 35.3 1.1 6 * 38 39.5 0.9 6 * 39 37.5 1.0 6 <- downstream
40 36.4 0.8 5 * 41 37.5 0.9 5 * 42 32.3 1.0 4 * 43 34.8 1.1 5 <- downstream
44 31.6 1.0 4 * 45 37.7 0.9 5 * 46 35.7 1.1 6 * 47 34.3 1.2 5 <- downstream
48 37.8 1.1 6 * 49 36.9 0.9 5 * 50 36.1 1.0 5 * 51 34.5 1.2 5 <- downstream
52 32.3 1.0 4 * 53 31.6 1.0 4 * 54 33.6 0.9 4 * 55 31.6 1.1 4 <- downstream
56 34.3 1.1 5 * 57 31.9 0.9 4 * 58 33.7 0.9 4 * 59 31.5 1.2 4 <- downstream
60 30.6 1.1 5 * 61 30.2 1.1 4 * 62 17.3 1.1 3 * 63 25.7 1.1 3 <- downstream
64 21.9 0.8 2 * 65 22.8 0.8 2 * 66 256.0 1.0 0 * 67 255.9 1.0 0 <- downstream (2 unused bins - interference?)
68 255.9 1.0 0 * 69 19.5 1.1 3 * 70 25.8 0.9 3 * 71 23.1 1.0 3 <- downstream (1 unused bin - interference?)
72 23.3 1.0 3 * 73 16.9 1.2 4 * 74 21.7 0.8 2 * 75 23.2 0.7 2 <- downstream
76 22.0 1.0 3 * 77 25.3 0.7 2 * 78 24.7 0.7 2 * 79 20.8 0.9 2 <- downstream
80 19.1 1.0 2 * 81 255.9 1.0 0 * 82 256.0 1.0 0 * 83 255.9 1.0 0 <- downstream [END]
84 0.1 1.0 0 * 85 255.8 1.0 0 * 86 255.8 1.0 0 * 87 255.9 1.0 0 <- unused
88 256.0 1.0 0 * 89 256.0 1.0 0 * 90 255.9 1.0 0 * 91 255.9 1.0 0 <- unused
92 256.0 1.0 0 * 93 255.9 1.0 0 * 94 255.8 1.0 0 * 95 255.3 1.0 0
96 0.1 1.0 0 * 97 255.6 1.0 0 * 98 255.8 1.0 0 * 99 255.9 1.0 0 higher frequencies suffer greater
100 255.9 1.0 0 * 101 255.8 1.0 0 * 102 255.8 1.0 0 * 103 0.0 1.0 0 loss rates over longer lines
104 255.8 1.0 0 * 105 255.7 1.0 0 * 106 255.2 1.0 0 * 107 255.6 1.0 0
108 255.6 1.0 0 * 109 254.6 1.0 0 * 110 255.9 1.0 0 * 111 254.6 1.0 0
112 254.7 1.0 0 * 113 255.4 1.0 0 * 114 254.7 1.0 0 * 115 255.2 1.0 0
116 256.0 1.0 0 * 117 256.0 1.0 0 * 118 256.0 1.0 0 * 119 256.0 1.0 0
120 256.0 1.0 0 * 121 256.0 1.0 0 * 122 256.0 1.0 0 * 123 256.0 1.0 0
124 256.0 1.0 0 * 125 256.0 1.0 0 * 126 256.0 1.0 0 * 127 256.0 1.0 0
128 256.0 1.0 0 * 129 256.0 1.0 0 * 130 256.0 1.0 0 * 131 256.0 1.0 0
132 256.0 1.0 0 * 133 256.0 1.0 0 * 134 256.0 1.0 0 * 135 256.0 1.0 0
136 256.0 1.0 0 * 137 256.0 1.0 0 * 138 256.0 1.0 0 * 139 256.0 1.0 0
140 256.0 1.0 0 * 141 256.0 1.0 0 * 142 256.0 1.0 0 * 143 256.0 1.0 0
144 256.0 1.0 0 * 145 256.0 1.0 0 * 146 256.0 1.0 0 * 147 256.0 1.0 0
148 256.0 1.0 0 * 149 256.0 1.0 0 * 150 256.0 1.0 0 * 151 256.0 1.0 0
152 256.0 1.0 0 * 153 256.0 1.0 0 * 154 256.0 1.0 0 * 155 256.0 1.0 0
156 256.0 1.0 0 * 157 256.0 1.0 0 * 158 256.0 1.0 0 * 159 256.0 1.0 0
160 256.0 1.0 0 * 161 256.0 1.0 0 * 162 256.0 1.0 0 * 163 256.0 1.0 0
164 256.0 1.0 0 * 165 256.0 1.0 0 * 166 256.0 1.0 0 * 167 256.0 1.0 0
168 256.0 1.0 0 * 169 256.0 1.0 0 * 170 256.0 1.0 0 * 171 256.0 1.0 0
172 256.0 1.0 0 * 173 256.0 1.0 0 * 174 256.0 1.0 0 * 175 256.0 1.0 0
176 256.0 1.0 0 * 177 256.0 1.0 0 * 178 256.0 1.0 0 * 179 256.0 1.0 0
180 256.0 1.0 0 * 181 256.0 1.0 0 * 182 256.0 1.0 0 * 183 256.0 1.0 0
184 256.0 1.0 0 * 185 256.0 1.0 0 * 186 256.0 1.0 0 * 187 256.0 1.0 0
188 256.0 1.0 0 * 189 256.0 1.0 0 * 190 256.0 1.0 0 * 191 256.0 1.0 0
192 256.0 1.0 0 * 193 256.0 1.0 0 * 194 256.0 1.0 0 * 195 256.0 1.0 0
196 256.0 1.0 0 * 197 256.0 1.0 0 * 198 256.0 1.0 0 * 199 256.0 1.0 0
200 256.0 1.0 0 * 201 256.0 1.0 0 * 202 256.0 1.0 0 * 203 256.0 1.0 0
204 256.0 1.0 0 * 205 256.0 1.0 0 * 206 256.0 1.0 0 * 207 256.0 1.0 0
208 256.0 1.0 0 * 209 256.0 1.0 0 * 210 256.0 1.0 0 * 211 256.0 1.0 0
212 256.0 1.0 0 * 213 256.0 1.0 0 * 214 256.0 1.0 0 * 215 256.0 1.0 0
216 256.0 1.0 0 * 217 256.0 1.0 0 * 218 256.0 1.0 0 * 219 256.0 1.0 0
220 256.0 1.0 0 * 221 256.0 1.0 0 * 222 256.0 1.0 0 * 223 256.0 1.0 0
224 256.0 1.0 0 * 225 256.0 1.0 0 * 226 256.0 1.0 0 * 227 256.0 1.0 0
228 256.0 1.0 0 * 229 256.0 1.0 0 * 230 256.0 1.0 0 * 231 256.0 1.0 0
232 256.0 1.0 0 * 233 256.0 1.0 0 * 234 256.0 1.0 0 * 235 256.0 1.0 0
236 256.0 1.0 0 * 237 256.0 1.0 0 * 238 256.0 1.0 0 * 239 256.0 1.0 0
240 256.0 1.0 0 * 241 256.0 1.0 0 * 242 256.0 1.0 0 * 243 256.0 1.0 0
244 256.0 1.0 0 * 245 256.0 1.0 0 * 246 256.0 1.0 0 * 247 256.0 1.0 0
248 256.0 1.0 0 * 249 256.0 1.0 0 * 250 256.0 1.0 0 * 251 256.0 1.0 0
252 256.0 1.0 0 * 253 256.0 1.0 0 * 254 256.0 1.0 0 * 255 256.0 1.0 0
--- ----- ---- -- - --- ----- ---- -- - --- ----- ---- -- - --- ----- ---- --
Bin SNR Gain Bi - Bin SNR Gain Bi - Bin SNR Gain Bi - Bin SNR Gain Bi
dB dB ts dB dB ts dB dB ts dB dB ts
Graphical with SNRSummary
ADSL statisticsFigures in brackets have been shown to provide a stable service in practice.
External linksReferences
|
||||||||||||||||||||
