Special function defined by an integral
Plot of the exponential integral function E n(z) with n=2 in the complex plane from -2-2i to 2+2i with colors created with Mathematica 13.1 function ComplexPlot3D In mathematics, the exponential integral Ei is a special function on the complex plane .
It is defined as one particular definite integral of the ratio between an exponential function and its argument .
Definitions
For real non-zero values of x , the exponential integral Ei(x ) is defined as
Ei
(
x
)
=
−
∫
−
x
∞
e
−
t
t
d
t
=
∫
−
∞
x
e
t
t
d
t
.
{\displaystyle \operatorname {Ei} (x)=-\int _{-x}^{\infty }{\frac {e^{-t}}{t}}\,dt=\int _{-\infty }^{x}{\frac {e^{t}}{t}}\,dt.}
[ 1]
lim
δ
→
0
+
E
1
(
−
x
±
i
δ
)
=
−
Ei
(
x
)
∓
i
π
,
x
>
0.
{\displaystyle \lim _{\delta \to 0+}E_{1}(-x\pm i\delta )=-\operatorname {Ei} (x)\mp i\pi ,\qquad x>0.}
Properties
Several properties of the exponential integral below, in certain cases, allow one to avoid its explicit evaluation through the definition above.
Convergent series
Plot of
E
1
{\displaystyle E_{1}}
Ei
{\displaystyle \operatorname {Ei} }
For real or complex arguments off the negative real axis,
E
1
(
z
)
{\displaystyle E_{1}(z)}
[ 2]
E
1
(
z
)
=
−
γ
−
ln
z
−
∑
k
=
1
∞
(
−
z
)
k
k
k
!
(
|
Arg
(
z
)
|
<
π
)
{\displaystyle E_{1}(z)=-\gamma -\ln z-\sum _{k=1}^{\infty }{\frac {(-z)^{k}}{k\;k!}}\qquad (\left|\operatorname {Arg} (z)\right|<\pi )}
where
γ
{\displaystyle \gamma }
Euler–Mascheroni constant . The sum converges for all complex
z
{\displaystyle z}
complex logarithm having a branch cut along the negative real axis.
This formula can be used to compute
E
1
(
x
)
{\displaystyle E_{1}(x)}
x
{\displaystyle x}
x
>
2.5
{\displaystyle x>2.5}
cancellation .
A faster converging series was found by Ramanujan :[ 3]
E
i
(
x
)
=
γ
+
ln
x
+
exp
(
x
/
2
)
∑
n
=
1
∞
(
−
1
)
n
−
1
x
n
n
!
2
n
−
1
∑
k
=
0
⌊
(
n
−
1
)
/
2
⌋
1
2
k
+
1
{\displaystyle {\rm {Ei}}(x)=\gamma +\ln x+\exp {(x/2)}\sum _{n=1}^{\infty }{\frac {(-1)^{n-1}x^{n}}{n!\,2^{n-1}}}\sum _{k=0}^{\lfloor (n-1)/2\rfloor }{\frac {1}{2k+1}}}
Relative error of the asymptotic approximation for different number
N
{\displaystyle ~N~}
Unfortunately, the convergence of the series above is slow for arguments of larger modulus. For example, more than 40 terms are required to get an answer correct to three significant figures for
E
1
(
10
)
{\displaystyle E_{1}(10)}
[ 4]
x
e
x
E
1
(
x
)
{\displaystyle xe^{x}E_{1}(x)}
[ 5]
E
1
(
x
)
=
exp
(
−
x
)
x
(
∑
n
=
0
N
−
1
n
!
(
−
x
)
n
+
O
(
N
!
x
−
N
)
)
{\displaystyle E_{1}(x)={\frac {\exp(-x)}{x}}\left(\sum _{n=0}^{N-1}{\frac {n!}{(-x)^{n}}}+O(N!x^{-N})\right)}
The relative error of the approximation above is plotted on the figure to the right for various values of
N
{\displaystyle N}
N
=
1
{\displaystyle N=1}
N
=
5
{\displaystyle N=5}
Asymptotics beyond all orders
Using integration by parts, we can obtain an explicit formula[ 6]
Ei
(
z
)
=
e
z
z
(
∑
k
=
0
n
k
!
z
k
+
e
n
(
z
)
)
,
e
n
(
z
)
≡
(
n
+
1
)
!
z
e
−
z
∫
−
∞
z
e
t
t
n
+
2
d
t
{\displaystyle \operatorname {Ei} (z)={\frac {e^{z}}{z}}\left(\sum _{k=0}^{n}{\frac {k!}{z^{k}}}+e_{n}(z)\right),\quad e_{n}(z)\equiv (n+1)!\ ze^{-z}\int _{-\infty }^{z}{\frac {e^{t}}{t^{n+2}}}\,dt}
z
{\displaystyle z}
|
e
n
(
z
)
|
{\displaystyle |e_{n}(z)|}
n
∼
|
z
|
{\displaystyle n\sim |z|}
|
e
n
(
z
)
|
≤
2
π
|
z
|
e
−
|
z
|
{\displaystyle \vert e_{n}(z)\vert \leq {\sqrt {\frac {2\pi }{\vert z\vert }}}e^{-\vert z\vert }}
Exponential and logarithmic behavior: bracketing
Bracketing of
E
1
{\displaystyle E_{1}}
From the two series suggested in previous subsections, it follows that
E
1
{\displaystyle E_{1}}
E
1
{\displaystyle E_{1}}
[ 7]
1
2
e
−
x
ln
(
1
+
2
x
)
<
E
1
(
x
)
<
e
−
x
ln
(
1
+
1
x
)
x
>
0
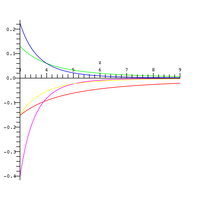
{\displaystyle {\frac {1}{2}}e^{-x}\,\ln \!\left(1+{\frac {2}{x}}\right)<E_{1}(x)<e^{-x}\,\ln \!\left(1+{\frac {1}{x}}\right)\qquad x>0}
The left-hand side of this inequality is shown in the graph to the left in blue; the central part
E
1
(
x
)
{\displaystyle E_{1}(x)}
Definition by Ein
Both
Ei
{\displaystyle \operatorname {Ei} }
E
1
{\displaystyle E_{1}}
entire function
Ein
{\displaystyle \operatorname {Ein} }
[ 8]
Ein
(
z
)
=
∫
0
z
(
1
−
e
−
t
)
d
t
t
=
∑
k
=
1
∞
(
−
1
)
k
+
1
z
k
k
k
!
{\displaystyle \operatorname {Ein} (z)=\int _{0}^{z}(1-e^{-t}){\frac {dt}{t}}=\sum _{k=1}^{\infty }{\frac {(-1)^{k+1}z^{k}}{k\;k!}}}
(note that this is just the alternating series in the above definition of
E
1
{\displaystyle E_{1}}
E
1
(
z
)
=
−
γ
−
ln
z
+
E
i
n
(
z
)
|
Arg
(
z
)
|
<
π
{\displaystyle E_{1}(z)\,=\,-\gamma -\ln z+{\rm {Ein}}(z)\qquad \left|\operatorname {Arg} (z)\right|<\pi }
Ei
(
x
)
=
γ
+
ln
x
−
Ein
(
−
x
)
x
≠
0
{\displaystyle \operatorname {Ei} (x)\,=\,\gamma +\ln {x}-\operatorname {Ein} (-x)\qquad x\neq 0}
The function
Ein
{\displaystyle \operatorname {Ein} }
harmonic numbers :
Ein
(
z
)
=
e
−
z
∑
n
=
1
∞
z
n
n
!
H
n
{\displaystyle \operatorname {Ein} (z)=e^{-z}\,\sum _{n=1}^{\infty }{\frac {z^{n}}{n!}}H_{n}}
Relation with other functions
Kummer's equation
z
d
2
w
d
z
2
+
(
b
−
z
)
d
w
d
z
−
a
w
=
0
{\displaystyle z{\frac {d^{2}w}{dz^{2}}}+(b-z){\frac {dw}{dz}}-aw=0}
is usually solved by the confluent hypergeometric functions
M
(
a
,
b
,
z
)
{\displaystyle M(a,b,z)}
U
(
a
,
b
,
z
)
.
{\displaystyle U(a,b,z).}
a
=
0
{\displaystyle a=0}
b
=
1
,
{\displaystyle b=1,}
z
d
2
w
d
z
2
+
(
1
−
z
)
d
w
d
z
=
0
{\displaystyle z{\frac {d^{2}w}{dz^{2}}}+(1-z){\frac {dw}{dz}}=0}
we have
M
(
0
,
1
,
z
)
=
U
(
0
,
1
,
z
)
=
1
{\displaystyle M(0,1,z)=U(0,1,z)=1}
for all z . A second solution is then given by E1 (−z ). In fact,
E
1
(
−
z
)
=
−
γ
−
i
π
+
∂
[
U
(
a
,
1
,
z
)
−
M
(
a
,
1
,
z
)
]
∂
a
,
0
<
A
r
g
(
z
)
<
2
π
{\displaystyle E_{1}(-z)=-\gamma -i\pi +{\frac {\partial [U(a,1,z)-M(a,1,z)]}{\partial a}},\qquad 0<{\rm {Arg}}(z)<2\pi }
with the derivative evaluated at
a
=
0.
{\displaystyle a=0.}
E1 is an exponential times the function U (1,1,z ):
E
1
(
z
)
=
e
−
z
U
(
1
,
1
,
z
)
{\displaystyle E_{1}(z)=e^{-z}U(1,1,z)}
The exponential integral is closely related to the logarithmic integral function li(x ) by the formula
li
(
e
x
)
=
Ei
(
x
)
{\displaystyle \operatorname {li} (e^{x})=\operatorname {Ei} (x)}
for non-zero real values of
x
{\displaystyle x}
Generalization
The exponential integral may also be generalized to
E
n
(
x
)
=
∫
1
∞
e
−
x
t
t
n
d
t
,
{\displaystyle E_{n}(x)=\int _{1}^{\infty }{\frac {e^{-xt}}{t^{n}}}\,dt,}
which can be written as a special case of the upper incomplete gamma function :[ 9]
E
n
(
x
)
=
x
n
−
1
Γ
(
1
−
n
,
x
)
.
{\displaystyle E_{n}(x)=x^{n-1}\Gamma (1-n,x).}
The generalized form is sometimes called the Misra function[ 10]
φ
m
(
x
)
{\displaystyle \varphi _{m}(x)}
φ
m
(
x
)
=
E
−
m
(
x
)
.
{\displaystyle \varphi _{m}(x)=E_{-m}(x).}
Many properties of this generalized form can be found in the NIST Digital Library of Mathematical Functions.
Including a logarithm defines the generalized integro-exponential function[ 11]
E
s
j
(
z
)
=
1
Γ
(
j
+
1
)
∫
1
∞
(
log
t
)
j
e
−
z
t
t
s
d
t
.
{\displaystyle E_{s}^{j}(z)={\frac {1}{\Gamma (j+1)}}\int _{1}^{\infty }\left(\log t\right)^{j}{\frac {e^{-zt}}{t^{s}}}\,dt.}
Derivatives
The derivatives of the generalised functions
E
n
{\displaystyle E_{n}}
[ 12]
E
n
′
(
z
)
=
−
E
n
−
1
(
z
)
(
n
=
1
,
2
,
3
,
…
)
{\displaystyle E_{n}'(z)=-E_{n-1}(z)\qquad (n=1,2,3,\ldots )}
Note that the function
E
0
{\displaystyle E_{0}}
e
−
z
/
z
{\displaystyle e^{-z}/z}
[ 13]
Exponential integral of imaginary argument
E
1
(
i
x
)
{\displaystyle E_{1}(ix)}
x
{\displaystyle x}
If
z
{\displaystyle z}
E
1
(
z
)
=
∫
1
∞
e
−
t
z
t
d
t
{\displaystyle E_{1}(z)=\int _{1}^{\infty }{\frac {e^{-tz}}{t}}\,dt}
to get a relation with the trigonometric integrals
Si
{\displaystyle \operatorname {Si} }
Ci
{\displaystyle \operatorname {Ci} }
E
1
(
i
x
)
=
i
[
−
1
2
π
+
Si
(
x
)
]
−
Ci
(
x
)
(
x
>
0
)
{\displaystyle E_{1}(ix)=i\left[-{\tfrac {1}{2}}\pi +\operatorname {Si} (x)\right]-\operatorname {Ci} (x)\qquad (x>0)}
The real and imaginary parts of
E
1
(
i
x
)
{\displaystyle \mathrm {E} _{1}(ix)}
Approximations
There have been a number of approximations for the exponential integral function. These include:
The Swamee and Ohija approximation[ 14]
E
1
(
x
)
=
(
A
−
7.7
+
B
)
−
0.13
,
{\displaystyle E_{1}(x)=\left(A^{-7.7}+B\right)^{-0.13},}
A
=
ln
[
(
0.56146
x
+
0.65
)
(
1
+
x
)
]
B
=
x
4
e
7.7
x
(
2
+
x
)
3.7
{\displaystyle {\begin{aligned}A&=\ln \left[\left({\frac {0.56146}{x}}+0.65\right)(1+x)\right]\\B&=x^{4}e^{7.7x}(2+x)^{3.7}\end{aligned}}}
The Allen and Hastings approximation [ 14] [ 15]
E
1
(
x
)
=
{
−
ln
x
+
a
T
x
5
,
x
≤
1
e
−
x
x
b
T
x
3
c
T
x
3
,
x
≥
1
{\displaystyle E_{1}(x)={\begin{cases}-\ln x+{\textbf {a}}^{T}{\textbf {x}}_{5},&x\leq 1\\{\frac {e^{-x}}{x}}{\frac {{\textbf {b}}^{T}{\textbf {x}}_{3}}{{\textbf {c}}^{T}{\textbf {x}}_{3}}},&x\geq 1\end{cases}}}
a
≜
[
−
0.57722
,
0.99999
,
−
0.24991
,
0.05519
,
−
0.00976
,
0.00108
]
T
b
≜
[
0.26777
,
8.63476
,
18.05902
,
8.57333
]
T
c
≜
[
3.95850
,
21.09965
,
25.63296
,
9.57332
]
T
x
k
≜
[
x
0
,
x
1
,
…
,
x
k
]
T
{\displaystyle {\begin{aligned}{\textbf {a}}&\triangleq [-0.57722,0.99999,-0.24991,0.05519,-0.00976,0.00108]^{T}\\{\textbf {b}}&\triangleq [0.26777,8.63476,18.05902,8.57333]^{T}\\{\textbf {c}}&\triangleq [3.95850,21.09965,25.63296,9.57332]^{T}\\{\textbf {x}}_{k}&\triangleq [x^{0},x^{1},\dots ,x^{k}]^{T}\end{aligned}}}
The continued fraction expansion [ 15]
E
1
(
x
)
=
e
−
x
x
+
1
1
+
1
x
+
2
1
+
2
x
+
3
⋱
.
{\displaystyle E_{1}(x)={\cfrac {e^{-x}}{x+{\cfrac {1}{1+{\cfrac {1}{x+{\cfrac {2}{1+{\cfrac {2}{x+{\cfrac {3}{\ddots }}}}}}}}}}}}.}
The approximation of Barry et al. [ 16]
E
1
(
x
)
=
e
−
x
G
+
(
1
−
G
)
e
−
x
1
−
G
ln
[
1
+
G
x
−
1
−
G
(
h
+
b
x
)
2
]
,
{\displaystyle E_{1}(x)={\frac {e^{-x}}{G+(1-G)e^{-{\frac {x}{1-G}}}}}\ln \left[1+{\frac {G}{x}}-{\frac {1-G}{(h+bx)^{2}}}\right],}
h
=
1
1
+
x
x
+
h
∞
q
1
+
q
q
=
20
47
x
31
26
h
∞
=
(
1
−
G
)
(
G
2
−
6
G
+
12
)
3
G
(
2
−
G
)
2
b
b
=
2
(
1
−
G
)
G
(
2
−
G
)
G
=
e
−
γ
{\displaystyle {\begin{aligned}h&={\frac {1}{1+x{\sqrt {x}}}}+{\frac {h_{\infty }q}{1+q}}\\q&={\frac {20}{47}}x^{\sqrt {\frac {31}{26}}}\\h_{\infty }&={\frac {(1-G)(G^{2}-6G+12)}{3G(2-G)^{2}b}}\\b&={\sqrt {\frac {2(1-G)}{G(2-G)}}}\\G&=e^{-\gamma }\end{aligned}}}
γ
{\displaystyle \gamma }
Euler–Mascheroni constant .
Inverse function of the Exponential Integral
We can express the Inverse function of the exponential integral in power series form:[ 17]
∀
|
x
|
<
μ
ln
(
μ
)
,
E
i
−
1
(
x
)
=
∑
n
=
0
∞
x
n
n
!
P
n
(
ln
(
μ
)
)
μ
n
{\displaystyle \forall |x|<{\frac {\mu }{\ln(\mu )}},\quad \mathrm {Ei} ^{-1}(x)=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}{\frac {P_{n}(\ln(\mu ))}{\mu ^{n}}}}
where
μ
{\displaystyle \mu }
Ramanujan–Soldner constant and
(
P
n
)
{\displaystyle (P_{n})}
polynomial sequence defined by the following recurrence relation :
P
0
(
x
)
=
x
,
P
n
+
1
(
x
)
=
x
(
P
n
′
(
x
)
−
n
P
n
(
x
)
)
.
{\displaystyle P_{0}(x)=x,\ P_{n+1}(x)=x(P_{n}'(x)-nP_{n}(x)).}
For
n
>
0
{\displaystyle n>0}
deg
P
n
=
n
{\displaystyle \deg P_{n}=n}
P
n
(
x
)
=
(
d
d
t
)
n
−
1
(
t
e
x
E
i
(
t
+
x
)
−
E
i
(
x
)
)
n
|
t
=
0
.
{\displaystyle P_{n}(x)=\left.\left({\frac {\mathrm {d} }{\mathrm {d} t}}\right)^{n-1}\left({\frac {te^{x}}{\mathrm {Ei} (t+x)-\mathrm {Ei} (x)}}\right)^{n}\right|_{t=0}.}
Applications
Time-dependent heat transfer
Nonequilibrium groundwater flow in the Theis solution (called a well function )
Radiative transfer in stellar and planetary atmospheres
Radial diffusivity equation for transient or unsteady state flow with line sources and sinks
Solutions to the neutron transport equation in simplified 1-D geometries[ 18]
See also
Notes
^ Abramowitz and Stegun, p. 228, 5.1.7
^ Abramowitz and Stegun, p. 229, 5.1.11
^ Andrews and Berndt, p. 130, 24.16
^ Bleistein and Handelsman, p. 2
^ Bleistein and Handelsman, p. 3
^ O’Malley, Robert E. (2014), O'Malley, Robert E. (ed.), "Asymptotic Approximations" , Historical Developments in Singular Perturbations , Cham: Springer International Publishing, pp. 27– 51, doi :10.1007/978-3-319-11924-3_2 , ISBN 978-3-319-11924-3 , retrieved 2023-05-04 ^ Abramowitz and Stegun, p. 229, 5.1.20
^ Abramowitz and Stegun, p. 228, see footnote 3.
^ Abramowitz and Stegun, p. 230, 5.1.45
^ After Misra (1940), p. 178
^ Milgram (1985)
^ Abramowitz and Stegun, p. 230, 5.1.26
^ Abramowitz and Stegun, p. 229, 5.1.24
^ a b Giao, Pham Huy (2003-05-01). "Revisit of Well Function Approximation and An Easy Graphical Curve Matching Technique for Theis' Solution". Ground Water . 41 (3): 387– 390. Bibcode :2003GrWat..41..387G . doi :10.1111/j.1745-6584.2003.tb02608.x . ISSN 1745-6584 . PMID 12772832 . S2CID 31982931 . ^ a b Tseng, Peng-Hsiang; Lee, Tien-Chang (1998-02-26). "Numerical evaluation of exponential integral: Theis well function approximation". Journal of Hydrology . 205 (1– 2): 38– 51. Bibcode :1998JHyd..205...38T . doi :10.1016/S0022-1694(97)00134-0 . ^ Barry, D. A; Parlange, J. -Y; Li, L (2000-01-31). "Approximation for the exponential integral (Theis well function)". Journal of Hydrology . 227 (1– 4): 287– 291. Bibcode :2000JHyd..227..287B . doi :10.1016/S0022-1694(99)00184-5 . ^ "Inverse function of the Exponential Integral Ei-1 (x ) " . Mathematics Stack Exchange . Retrieved 2024-04-24 .^ George I. Bell; Samuel Glasstone (1970). Nuclear Reactor Theory . Van Nostrand Reinhold Company.
References
Abramowitz, Milton; Irene Stegun (1964). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables Abramowitz and Stegun . New York: Dover. ISBN 978-0-486-61272-0 Chapter 5 .Bender, Carl M.; Steven A. Orszag (1978). Advanced mathematical methods for scientists and engineers . McGraw–Hill. ISBN 978-0-07-004452-4 Bleistein, Norman; Richard A. Handelsman (1986). Asymptotic Expansions of Integrals . Dover. ISBN 978-0-486-65082-1 Andrews, George E.; Berndt, Bruce C. (2013), Ramanujan's lost notebook. Part IV , Berlin, New York: Springer-Verlag , ISBN 978-1-4614-4080-2 Busbridge, Ida W. (1950). "On the integro-exponential function and the evaluation of some integrals involving it". Quart. J. Math. (Oxford) . 1 (1): 176– 184. Bibcode :1950QJMat...1..176B . doi :10.1093/qmath/1.1.176 . Stankiewicz, A. (1968). "Tables of the integro-exponential functions". Acta Astronomica . 18 : 289. Bibcode :1968AcA....18..289S . Sharma, R. R.; Zohuri, Bahman (1977). "A general method for an accurate evaluation of exponential integrals E1 (x), x>0". J. Comput. Phys . 25 (2): 199– 204. Bibcode :1977JCoPh..25..199S . doi :10.1016/0021-9991(77)90022-5 . Kölbig, K. S. (1983). "On the integral exp(−μt )t ν−1 logm t dt " . Math. Comput . 41 (163): 171– 182. doi :10.1090/S0025-5718-1983-0701632-1 Milgram, M. S. (1985). "The generalized integro-exponential function" . Mathematics of Computation . 44 (170): 443– 458. doi :10.1090/S0025-5718-1985-0777276-4 JSTOR 2007964 . MR 0777276 . Misra, Rama Dhar; Born, M. (1940). "On the Stability of Crystal Lattices. II". Mathematical Proceedings of the Cambridge Philosophical Society . 36 (2): 173. Bibcode :1940PCPS...36..173M . doi :10.1017/S030500410001714X . S2CID 251097063 . Chiccoli, C.; Lorenzutta, S.; Maino, G. (1988). "On the evaluation of generalized exponential integrals Eν (x)". J. Comput. Phys . 78 (2): 278– 287. Bibcode :1988JCoPh..78..278C . doi :10.1016/0021-9991(88)90050-2 . Chiccoli, C.; Lorenzutta, S.; Maino, G. (1990). "Recent results for generalized exponential integrals" . Computer Math. Applic . 19 (5): 21– 29. doi :10.1016/0898-1221(90)90098-5 . MacLeod, Allan J. (2002). "The efficient computation of some generalised exponential integrals" . J. Comput. Appl. Math . 148 (2): 363– 374. Bibcode :2002JCoAM.148..363M . doi :10.1016/S0377-0427(02)00556-3 Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 6.3. Exponential Integrals" , Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8 the original on 2011-08-11, retrieved 2011-08-09 Temme, N. M. (2010), "Exponential, Logarithmic, Sine, and Cosine Integrals" , in Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248
External links








































![{\displaystyle E_{1}(-z)=-\gamma -i\pi +{\frac {\partial [U(a,1,z)-M(a,1,z)]}{\partial a}},\qquad 0<{\rm {Arg}}(z)<2\pi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/baf776ea1a2dea96558b4a7f2cf7bae3d8cad7ac)
















![{\displaystyle E_{1}(ix)=i\left[-{\tfrac {1}{2}}\pi +\operatorname {Si} (x)\right]-\operatorname {Ci} (x)\qquad (x>0)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc6245104e0362c31571f3abda13b3f5f06d06c9)


![{\displaystyle {\begin{aligned}A&=\ln \left[\left({\frac {0.56146}{x}}+0.65\right)(1+x)\right]\\B&=x^{4}e^{7.7x}(2+x)^{3.7}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2fee0fd224536a437d20c1e057ed6ed4187b21d)

![{\displaystyle {\begin{aligned}{\textbf {a}}&\triangleq [-0.57722,0.99999,-0.24991,0.05519,-0.00976,0.00108]^{T}\\{\textbf {b}}&\triangleq [0.26777,8.63476,18.05902,8.57333]^{T}\\{\textbf {c}}&\triangleq [3.95850,21.09965,25.63296,9.57332]^{T}\\{\textbf {x}}_{k}&\triangleq [x^{0},x^{1},\dots ,x^{k}]^{T}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd59588e32d86da6a1545610b3b27d9f8ec38b7f)

![{\displaystyle E_{1}(x)={\frac {e^{-x}}{G+(1-G)e^{-{\frac {x}{1-G}}}}}\ln \left[1+{\frac {G}{x}}-{\frac {1-G}{(h+bx)^{2}}}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f90bab5b2a5c683e40d3dbf066bf2b79160d692b)







