|
Database transaction schedule
In the fields of databases and transaction processing (transaction management), a schedule (or history) of a system is an abstract model to describe the order of executions in a set of transactions running in the system. Often it is a list of operations (actions) ordered by time, performed by a set of transactions that are executed together in the system. If the order in time between certain operations is not determined by the system, then a partial order is used. Examples of such operations are requesting a read operation, reading, writing, aborting, committing, requesting a lock, locking, etc. Often, only a subset of the transaction operation types are included in a schedule. Schedules are fundamental concepts in database concurrency control theory. In practice, most general purpose database systems employ conflict-serializable and strict recoverable schedules. NotationGrid notation:
Operations (a.k.a., actions):
Alternatively, a schedule can be represented with a directed acyclic graph (or DAG) in which there is an arc (i.e., directed edge) between each ordered pair of operations. ExampleThe following is an example of a schedule:
In this example, the columns represent the different transactions in the schedule D. Schedule D consists of three transactions T1, T2, T3. First T1 Reads and Writes to object X, and then Commits. Then T2 Reads and Writes to object Y and Commits, and finally, T3 Reads and Writes to object Z and Commits. The schedule D above can be represented as list in the following way: D = R1(X) W1(X) Com1 R2(Y) W2(Y) Com2 R3(Z) W3(Z) Com3 Duration and order of actionsUsually, for the purpose of reasoning about concurrency control in databases, an operation is modelled as atomic, occurring at a point in time, without duration. Real executed operations always have some duration. Operations of transactions in a schedule can interleave (i.e., transactions can be executed concurrently), but time orders between operations in each transaction must remain unchanged. The schedule is in partial order when the operations of transactions in a schedule interleave (i.e., when the schedule is conflict-serializable but not serial). The schedule is in total order when the operations of transactions in a schedule do not interleave (i.e., when the schedule is serial). Types of scheduleA complete schedule is one that contains either an abort (a.k.a. rollback) or commit action for each of its transactions. A transaction's last action is either to commit or abort. To maintain atomicity, a transaction must undo all its actions if it is aborted. SerialA schedule is serial if the executed transactions are non-interleaved (i.e., a serial schedule is one in which no transaction starts until a running transaction has ended). Schedule D is an example of a serial schedule:
SerializableA schedule is serializable if it is equivalent (in its outcome) to a serial schedule. In schedule E, the order in which the actions of the transactions are executed is not the same as in D, but in the end, E gives the same result as D.
Serializability is used to keep the data in the data item in a consistent state. It is the major criterion for the correctness of concurrent transactions' schedule, and thus supported in all general purpose database systems. Schedules that are not serializable are likely to generate erroneous outcomes; which can be extremely harmful (e.g., when dealing with money within banks).[1][2][3] If any specific order between some transactions is requested by an application, then it is enforced independently of the underlying serializability mechanisms. These mechanisms are typically indifferent to any specific order, and generate some unpredictable partial order that is typically compatible with multiple serial orders of these transactions. Conflicting actionsTwo actions are said to be in conflict (conflicting pair) if and only if all of the 3 following conditions are satisfied:
Equivalently, two actions are considered conflicting if and only if they are noncommutative. Equivalently, two actions are considered conflicting if and only if they are a read-write, write-read, or write-write conflict. The following set of actions is conflicting:
While the following sets of actions are not conflicting:
Reducing conflicts, such as through commutativity, enhances performance because conflicts are the fundamental cause of delays and aborts. The conflict is materialized if the requested conflicting operation is actually executed: in many cases a requested/issued conflicting operation by a transaction is delayed and even never executed, typically by a lock on the operation's object, held by another transaction, or when writing to a transaction's temporary private workspace and materializing, copying to the database itself, upon commit; as long as a requested/issued conflicting operation is not executed upon the database itself, the conflict is non-materialized; non-materialized conflicts are not represented by an edge in the precedence graph. Conflict equivalenceThe schedules S1 and S2 are said to be conflict-equivalent if and only if both of the following two conditions are satisfied:
Equivalently, two schedules are said to be conflict equivalent if and only if one can be transformed to another by swapping pairs of non-conflicting operations (whether adjacent or not) while maintaining the order of actions for each transaction.[4] Equivalently, two schedules are said to be conflict equivalent if and only if one can be transformed to another by swapping pairs of non-conflicting adjacent operations with different transactions.[7] Conflict-serializableA schedule is said to be conflict-serializable when the schedule is conflict-equivalent to one or more serial schedules. Equivalently, a schedule is conflict-serializable if and only if its precedence graph is acyclic when only committed transactions are considered. Note that if the graph is defined to also include uncommitted transactions, then cycles involving uncommitted transactions may occur without conflict serializability violation. The schedule K is conflict-equivalent to the serial schedule <T1,T2>, but not <T2,T1>.
Conflict serializability can be enforced by restarting any transaction within the cycle in the precedence graph, or by implementing two-phase locking, timestamp ordering, or serializable snapshot isolation.[8] View equivalenceTwo schedules S1 and S2 are said to be view-equivalent when the following conditions are satisfied:
Additionally, two view-equivalent schedules must involve the same set of transactions such that each transaction has the same actions in the same order. In the example below, the schedules S1 and S2 are view-equivalent, but neither S1 nor S2 are view-equivalent to the schedule S3.
The conditions for S3 to be view-equivalent to S1 and S2 were not satisfied at the corresponding superscripts for the following reasons:
To quickly analyze whether two schedules are view-equivalent, write both schedules as a list with each action's subscript representing which view-equivalence condition they match. The schedules are view equivalent if and only if all the actions have the same subscript (or lack thereof) in both schedules:
View-serializableA schedule is view-serializable if it is view-equivalent to some serial schedule. Note that by definition, all conflict-serializable schedules are view-serializable.
Notice that the above example (which is the same as the example in the discussion of conflict-serializable) is both view-serializable and conflict-serializable at the same time. There are however view-serializable schedules that are not conflict-serializable: those schedules with a transaction performing a blind write:
The above example is not conflict-serializable, but it is view-serializable since it has a view-equivalent serial schedule <T1,| T2,| T3>. Since determining whether a schedule is view-serializable is NP-complete, view-serializability has little practical interest.[citation needed] RecoverableIn a recoverable schedule, transactions only commit after all transactions whose changes they read have committed. A schedule becomes unrecoverable if a transaction reads and relies on changes from another transaction , and then commits and aborts.
These schedules are recoverable. The schedule F is recoverable because T1 commits before T2, that makes the value read by T2 correct. Then T2 can commit itself. In the F2 schedule, if T1 aborted, T2 has to abort because the value of A it read is incorrect. In both cases, the database is left in a consistent state. Schedule J is unrecoverable because T2 committed before T1 despite previously reading the value written by T1. Because T1 aborted after T2 committed, the value read by T2 is wrong. Because a transaction cannot be rolled-back after it commits, the schedule is unrecoverable. CascadelessCascadeless schedules (a.k.a, "Avoiding Cascading Aborts (ACA) schedules") are schedules which avoid cascading aborts by disallowing dirty reads. Cascading aborts occur when one transaction's abort causes another transaction to abort because it read and relied on the first transaction's changes to an object. A dirty read occurs when a transaction reads data from uncommitted write in another transaction.[9] The following examples are the same as the ones in the discussion on recoverable:
In this example, although F2 is recoverable, it does not avoid cascading aborts. It can be seen that if T1 aborts, T2 will have to be aborted too in order to maintain the correctness of the schedule as T2 has already read the uncommitted value written by T1. The following is a recoverable schedule which avoids cascading abort. Note, however, that the update of A by T1 is always lost (since T1 is aborted).
Note that this Schedule would not be serializable if T1 would be committed. Cascading aborts avoidance is sufficient but not necessary for a schedule to be recoverable. StrictA schedule is strict if for any two transactions T1, T2, if a write operation of T1 precedes a conflicting operation of T2 (either read or write), then the commit or abort event of T1 also precedes that conflicting operation of T2. For example, the schedule F3 above is strict. Any strict schedule is cascade-less, but not the converse. Strictness allows efficient recovery of databases from failure. Serializability Class RelationshipsThe following expressions illustrate the hierarchical (containment) relationships between serializability and recoverability classes:
The Venn diagram (below) illustrates the above clauses graphically. 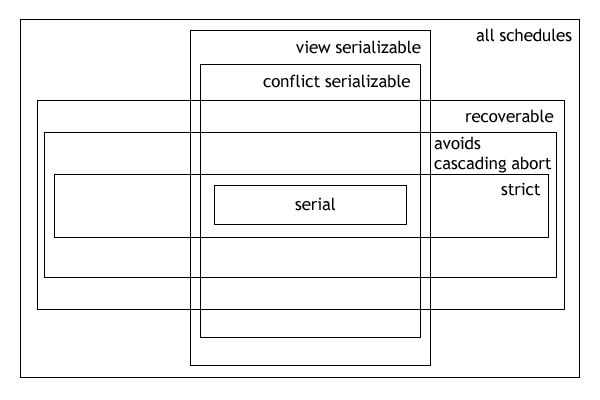 See also
References
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||




