|
Conservative vector field
In vector calculus, a conservative vector field is a vector field that is the gradient of some function.[1] A conservative vector field has the property that its line integral is path independent; the choice of path between two points does not change the value of the line integral. Path independence of the line integral is equivalent to the vector field under the line integral being conservative. A conservative vector field is also irrotational; in three dimensions, this means that it has vanishing curl. An irrotational vector field is necessarily conservative provided that the domain is simply connected. Conservative vector fields appear naturally in mechanics: They are vector fields representing forces of physical systems in which energy is conserved.[2] For a conservative system, the work done in moving along a path in a configuration space depends on only the endpoints of the path, so it is possible to define potential energy that is independent of the actual path taken. Informal treatmentIn a two- and three-dimensional space, there is an ambiguity in taking an integral between two points as there are infinitely many paths between the two points—apart from the straight line formed between the two points, one could choose a curved path of greater length as shown in the figure. Therefore, in general, the value of the integral depends on the path taken. However, in the special case of a conservative vector field, the value of the integral is independent of the path taken, which can be thought of as a large-scale cancellation of all elements that do not have a component along the straight line between the two points. To visualize this, imagine two people climbing a cliff; one decides to scale the cliff by going vertically up it, and the second decides to walk along a winding path that is longer in length than the height of the cliff, but at only a small angle to the horizontal. Although the two hikers have taken different routes to get up to the top of the cliff, at the top, they will have both gained the same amount of gravitational potential energy. This is because a gravitational field is conservative.  Intuitive explanationM. C. Escher's lithograph print Ascending and Descending illustrates a non-conservative vector field, impossibly made to appear to be the gradient of the varying height above ground (gravitational potential) as one moves along the staircase. The force field experienced by the one moving on the staircase is non-conservative in that one can return to the starting point while ascending more than one descends or vice versa, resulting in nonzero work done by gravity. On a real staircase, the height above the ground is a scalar potential field: one has to go upward exactly as much as one goes downward in order to return to the same place, in which case the work by gravity totals to zero. This suggests path-independence of work done on the staircase; equivalently, the force field experienced is conservative (see the later section: Path independence and conservative vector field). The situation depicted in the print is impossible. DefinitionA vector field , where is an open subset of , is said to be conservative if there exists a (continuously differentiable) scalar field [3] on such that
Here, denotes the gradient of . Since is continuously differentiable, is continuous. When the equation above holds, is called a scalar potential for . The fundamental theorem of vector calculus states that, under some regularity conditions, any vector field can be expressed as the sum of a conservative vector field and a solenoidal field. Path independence and conservative vector fieldPath independenceA line integral of a vector field is said to be path-independent if it depends on only two integral path endpoints regardless of which path between them is chosen:[4] for any pair of integral paths and between a given pair of path endpoints in . The path independence is also equivalently expressed as for any piecewise smooth closed path in where the two endpoints are coincident. Two expressions are equivalent since any closed path can be made by two path; from an endpoint to another endpoint , and from to , so where is the reverse of and the last equality holds due to the path independence Conservative vector fieldA key property of a conservative vector field is that its integral along a path depends on only the endpoints of that path, not the particular route taken. In other words, if it is a conservative vector field, then its line integral is path-independent. Suppose that for some (continuously differentiable) scalar field [3] over as an open subset of (so is a conservative vector field that is continuous) and is a differentiable path (i.e., it can be parameterized by a differentiable function) in with an initial point and a terminal point . Then the gradient theorem (also called fundamental theorem of calculus for line integrals) states that This holds as a consequence of the definition of a line integral, the chain rule, and the second fundamental theorem of calculus. in the line integral is an exact differential for an orthogonal coordinate system (e.g., Cartesian, cylindrical, or spherical coordinates). Since the gradient theorem is applicable for a differentiable path, the path independence of a conservative vector field over piecewise-differential curves is also proved by the proof per differentiable curve component.[5] So far it has been proven that a conservative vector field is line integral path-independent. Conversely, if a continuous vector field is (line integral) path-independent, then it is a conservative vector field, so the following biconditional statement holds:[4] For a continuous vector field , where is an open subset of , it is conservative if and only if its line integral along a path in is path-independent, meaning that the line integral depends on only both path endpoints regardless of which path between them is chosen.
The proof of this converse statement is the following.  is a continuous vector field which line integral is path-independent. Then, let's make a function defined as over an arbitrary path between a chosen starting point and an arbitrary point . Since it is path-independent, it depends on only and regardless of which path between these points is chosen. Let's choose the path shown in the left of the right figure where a 2-dimensional Cartesian coordinate system is used. The second segment of this path is parallel to the axis so there is no change along the axis. The line integral along this path is By the path independence, its partial derivative with respect to (for to have partial derivatives, needs to be continuous.) is since and are independent to each other. Let's express as where and are unit vectors along the and axes respectively, then, since , where the last equality is from the second fundamental theorem of calculus. A similar approach for the line integral path shown in the right of the right figure results in so is proved for the 2-dimensional Cartesian coordinate system. This proof method can be straightforwardly expanded to a higher dimensional orthogonal coordinate system (e.g., a 3-dimensional spherical coordinate system) so the converse statement is proved. Another proof is found here as the converse of the gradient theorem. Irrotational vector fields Let (3-dimensional space), and let be a (continuously differentiable) vector field, with an open subset of . Then is called irrotational if its curl is everywhere in , i.e., if For this reason, such vector fields are sometimes referred to as curl-free vector fields or curl-less vector fields. They are also referred to as longitudinal vector fields. It is an identity of vector calculus that for any (continuously differentiable up to the 2nd derivative) scalar field on , we have Therefore, every conservative vector field in is also an irrotational vector field in . This result can be easily proved by expressing in a Cartesian coordinate system with Schwarz's theorem (also called Clairaut's theorem on equality of mixed partials). Provided that is a simply connected open space (roughly speaking, a single piece open space without a hole within it), the converse of this is also true: Every irrotational vector field in a simply connected open space is a conservative vector field in . The above statement is not true in general if is not simply connected. Let be with removing all coordinates on the -axis (so not a simply connected space), i.e., . Now, define a vector field on by Then has zero curl everywhere in ( at everywhere in ), i.e., is irrotational. However, the circulation of around the unit circle in the -plane is ; in polar coordinates, , so the integral over the unit circle is Therefore, does not have the path-independence property discussed above so is not conservative even if since where is defined is not a simply connected open space. Say again, in a simply connected open region, an irrotational vector field has the path-independence property (so as conservative). This can be proved directly by using Stokes' theorem,for any smooth oriented surface which boundary is a simple closed path . So, it is concluded that In a simply connected open region, any vector field that has the path-independence property (so it is a conservative vector field.) must also be irrotational and vice versa. AbstractionMore abstractly, in the presence of a Riemannian metric, vector fields correspond to differential -forms. The conservative vector fields correspond to the exact -forms, that is, to the forms which are the exterior derivative of a function (scalar field) on . The irrotational vector fields correspond to the closed -forms, that is, to the -forms such that . As , any exact form is closed, so any conservative vector field is irrotational. Conversely, all closed -forms are exact if is simply connected. VorticityThe vorticity of a vector field can be defined by: The vorticity of an irrotational field is zero everywhere.[6] Kelvin's circulation theorem states that a fluid that is irrotational in an inviscid flow will remain irrotational. This result can be derived from the vorticity transport equation, obtained by taking the curl of the Navier–Stokes equations. For a two-dimensional field, the vorticity acts as a measure of the local rotation of fluid elements. The vorticity does not imply anything about the global behavior of a fluid. It is possible for a fluid that travels in a straight line to have vorticity, and it is possible for a fluid that moves in a circle to be irrotational. Conservative forces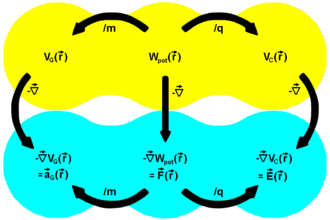
If the vector field associated to a force is conservative, then the force is said to be a conservative force. The most prominent examples of conservative forces are gravitational force (associated with a gravitational field) and electric force (associated with an electrostatic field). According to Newton's law of gravitation, a gravitational force acting on a mass due to a mass located at a distance from , obeys the equation
where is the gravitational constant and is a unit vector pointing from toward . The force of gravity is conservative because , where
is the gravitational potential energy. In other words, the gravitation field associated with the gravitational force is the gradient of the gravitation potential associated with the gravitational potential energy . It can be shown that any vector field of the form is conservative, provided that is integrable. For conservative forces, path independence can be interpreted to mean that the work done in going from a point to a point is independent of the moving path chosen (dependent on only the points and ), and that the work done in going around a simple closed loop is :
The total energy of a particle moving under the influence of conservative forces is conserved, in the sense that a loss of potential energy is converted to the equal quantity of kinetic energy, or vice versa. See also
References
Further reading
|


















































































