|
Clawson pointIn Euclidean geometry, the Clawson point is a special point in a triangle defined by the trilinear coordinates tan α : tan β : tan γ,[1] where α, β, γ are the interior angles at the triangle vertices A, B, C. It is named after John Wentworth Clawson, who published it 1925 in the American Mathematical Monthly. It is denoted X(19) in Clark Kimberling's Encyclopedia of Triangle Centers. Geometrical constructionsThere are at least two ways to construct the Clawson point, which also could be used as coordinate free definitions of the point. In both cases you have two triangles, where the three lines connecting their according vertices meet in a common point, which is the Clawson point. Construction 1 Reference triangle △ABC Perspective lines between △HAHBHC and △TATBTC, which are similar; meet at the homothetic center P (the Clawson point) For a given triangle △ABC, let △HAHBHC be its orthic triangle and △TATBTC the triangle formed by the outer tangents to its three excircles. These two triangles are similar and the Clawson point is their center of similarity, therefore the three lines TAHA, TBHB, TCHC connecting their vertices meet in a common point, which is the Clawson point.[2][3] Construction 2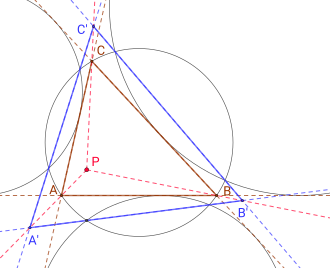 Reference triangle △ABC Triangle △A'B'C', formed by lines connecting pairs of intersection points between each excircle and the circumcircle For a triangle △ABC, its circumcircle intersects each of its three excircles in two points. The three lines through those points of intersections form a triangle △A'B'C'. This triangle and △ABC are perspective triangles with the Clawson point being their perspective center. Hence the three lines AA', BB', CC' meet in the Clawson point.[1] HistoryThe point is now named after J. W. Clawson, who published its trilinear coordinates 1925 in the American Mathematical Monthly as problem 3132, where he asked for geometrical construction of that point.[4] However the French mathematician Émile Lemoine had already examined the point in 1886.[5] Later the point was independently rediscovered by R. Lyness and G. R. Veldkamp in 1983, who called it crucial point after the Canadian math journal Crux Mathematicorum in which it was published as problem 682.[1] References
External links
|