|
Branched flow Branched flow refers to a phenomenon in wave dynamics, that produces a tree-like pattern involving successive mostly forward scattering events by smooth obstacles deflecting traveling rays or waves. Sudden and significant momentum or wavevector changes are absent, but accumulated small changes can lead to large momentum changes. The path of a single ray is less important than the environs around a ray, which rotate, compress, and stretch around in an area preserving way. Even more revealing are groups, or manifolds of neighboring rays extending over significant zones. Starting rays out from a point but varying their direction over a range, one to the next, or from different points along a line all with the same initial directions are examples of a manifold. Waves have analogous launching conditions, such as a point source spraying in many directions, or an extended plane wave heading on one direction. The ray bending or refraction leads to characteristic structure in phase space and nonuniform distributions in coordinate space that look somehow universal and resemble branches in trees or stream beds. The branches taken on non-obvious paths through the refracting landscape that are indirect and nonlocal results of terrain already traversed. For a given refracting landscape, the branches will look completely different depending on the initial manifold. ExamplesTwo-dimensional electron gasBranched flow was first identified in experiments with a two-dimensional electron gas.[1] Electrons flowing from a quantum point contact were scanned using a scanning probe microscope. Instead of usual diffraction patterns, the electrons flowed forming branching strands that persisted for several correlation lengths of the background potential. Ocean dynamicsFocusing of random waves in the ocean can also lead to branched flow.[2] The fluctuation in the depth of the ocean floor can be described as a random potential. A tsunami wave propagating in such medium will form branches which carry huge energy densities over long distances. This mechanism may also explain some statistical discrepancies in the occurrence of freak waves.[3] Light propagationGiven the wave nature of light, its propagation in random media can produce branched flow too.[4] Experiments with laser beams in soap bubbles have shown this effect, which has also been proposed to control light focusing in a disordered medium.[5] Flexural waves in elastic platesFlexural waves travelling in elastic plates also produce branched flows.[6] Disorder, in this case, appears in the form of inhomogeneous flexural rigidity. Other examplesOther examples where branched flow has been proposed to happen include microwave radiation of pulsars refracted by interstellar clouds,[7] the Zeldovitch model for the large structure of the universe and electron-phonon interaction in metals.[8] Dynamics: Kick and drift map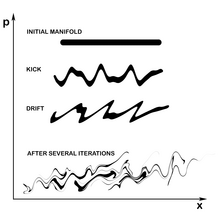 The dynamical mechanism that originates the branch formation can be understood by means of the kick and drift map, an area preserving map defined by: where n accounts for the discrete time, x and p are position and momentum respectively, and V is the potential. The equation for the momentum is called the “kick” stage, whereas the equation for the position is the “drift”. Given an initial manifold in phase space, it can be iterated under the action of the kick and drift map. Typically, the manifold stretches and folds (although keeping its total area constant) forming cusps or caustics and stable regions. These regions of phases space with high concentration of trajectories are precisely the branches. Scaling properties of branched flow in random potentialsWhen plane waves or parallel trajectories propagate through a weak random medium, several caustics can arise at more or less regularly ordered positions. Taking the direction perpendicular to the flow, the distance separating the caustics is determined by the correlation length of the potential d.[9][10] Another characteristic length is the distance L downstream where the first generation of caustics appear. Taking into account the energy of the trajectories E and the height of the potential ɛ<<E, it can be argued[9][10] that the following relation holds See also
References
External links |


