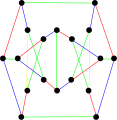
Two 3-regular graphs with 18 vertices and 27 edges
In the mathematical field of graph theory , the Blanuša snarks are two 3-regular graphs with 18 vertices and 27 edges.[ 2] Yugoslavian mathematician Danilo Blanuša in 1946 and are named after him.[ 3] Petersen graph .
As snarks , the Blanuša snarks are connected, bridgeless cubic graphs with chromatic index equal to 4. Both of them have chromatic number 3, diameter 4 and girth 5. They are non-hamiltonian but are hypohamiltonian .[ 4] book thickness 3 and queue number 2.[ 5]
Algebraic properties
The automorphism group of the first Blanuša snark is of order 8 and is isomorphic to the Dihedral group D 4 , the group of symmetries of a square.
The automorphism group of the second Blanuša snark is an abelian group of order 4 isomorphic to the Klein four-group , the direct product of the Cyclic group Z /2Z with itself.
The characteristic polynomial of the first and the second Blanuša snark are respectively :
(
x
−
3
)
(
x
−
1
)
3
(
x
+
1
)
(
x
+
2
)
(
x
4
+
x
3
−
7
x
2
−
5
x
+
6
)
(
x
4
+
x
3
−
5
x
2
−
3
x
+
4
)
2
{\displaystyle (x-3)(x-1)^{3}(x+1)(x+2)(x^{4}+x^{3}-7x^{2}-5x+6)(x^{4}+x^{3}-5x^{2}-3x+4)^{2}\ }
(
x
−
3
)
(
x
−
1
)
3
(
x
3
+
2
x
2
−
3
x
−
5
)
(
x
3
+
2
x
2
−
x
−
1
)
(
x
4
+
x
3
−
7
x
2
−
6
x
+
7
)
(
x
4
+
x
3
−
5
x
2
−
4
x
+
3
)
.
{\displaystyle (x-3)(x-1)^{3}(x^{3}+2x^{2}-3x-5)(x^{3}+2x^{2}-x-1)(x^{4}+x^{3}-7x^{2}-6x+7)(x^{4}+x^{3}-5x^{2}-4x+3).\ }
There exists a generalisation of the first and second Blanuša snark in two infinite families of snarks of order 8n +10 denoted
B
n
1
{\displaystyle B_{n}^{1}}
B
n
2
{\displaystyle B_{n}^{2}}
[ 6]
In 2007, J. Mazák proved that the circular chromatic index of the type 1 generalized Blanuša snarks
B
n
1
{\displaystyle B_{n}^{1}}
3
+
2
n
{\displaystyle 3+{\frac {2}{n}}}
[ 7]
In 2008, M. Ghebleh proved that the circular chromatic index of the type 2 generalized Blanuša snarks
B
n
2
{\displaystyle B_{n}^{2}}
3
+
1
⌊
1
+
3
n
/
2
⌋
{\displaystyle 3+{\frac {1}{\lfloor 1+3n/2\rfloor }}}
[ 8]
Gallery
References
^ Orbanić, Alen; Pisanski, Tomaž; Randić, Milan; Servatius, Brigitte (2004). "Blanuša double". Math. Commun. 9 (1): 91– 103. ^ Weisstein, Eric W. "Blanuša snarks" . MathWorld ^ Blanuša, D. , "Problem cetiriju boja." Glasnik Mat. Fiz. Astr. Ser. II. 1, 31-42, 1946.^ Eckhard Steen, "On Bicritical Snarks" Math. Slovaca, 1997.
^ Wolz, Jessica; Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
^ Read, R. C. and Wilson, R. J. An Atlas of Graphs. Oxford, England: Oxford University Press, pp. 276 and 280, 1998.
^ J. Mazák, Circular chromatic index of snarks, Master's thesis, Comenius University in Bratislava, 2007.
^ M. Ghebleh, Circular Chromatic Index of Generalized Blanuša Snarks, The Electronic Journal of Combinatorics, vol 15, 2008.