|
Barnette–Bosák–Lederberg graph
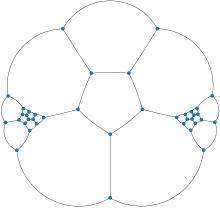
In the mathematical field of graph theory, the Barnette–Bosák–Lederberg graph is a cubic (that is, 3-regular) polyhedral graph with no Hamiltonian cycle, the smallest such graph possible.[1] It was discovered in the mid-1960s by Joshua Lederberg, David Barnette, and Juraj Bosák, after whom it is named. It has 38 vertices and 57 edges.[2][3][4] Other larger non-Hamiltonian cubic polyhedral graphs include the 46-vertex Tutte graph and a 44-vertex graph found by Emanuels Grīnbergs using Grinberg's theorem. The Barnette–Bosák–Lederberg graph has a similar construction to the Tutte graph but is composed of two Tutte fragments, connected through a pentagonal prism, instead of three connected through a tetrahedron. Without the constraint of having exactly three edges at every vertex, much smaller non-Hamiltonian polyhedral graphs are possible, including the Goldner–Harary graph and the Herschel graph. References
|
||||||||||||||||||||||