|
Schrägspiegelung Die Schrägspiegelung ist eine Verallgemeinerung der Achsenspiegelung. Die Verallgemeinerung darin besteht, dass ein Punkt nicht notwendig rechtwinklig, sondern in einer (z. B. durch einen Winkel oder einen Vektor) vorgegebenen Richtung an der Achse gespiegelt wird. Somit ist die gewöhnliche Achsenspiegelung ein Sonderfall der Schrägspiegelung. Merkmale der SchrägspiegelungDie Fixpunkte der Schrägspiegelung liegen wie bei der Achsenspiegelung auf der Spiegelachse, welche somit eine – und zwar die einzige – Fixpunktgerade ist. Weiterhin sind alle zum gegebenen Richtungsvektor parallelen Geraden Fixgeraden. Schrägspieglungen sind geraden- und flächentreu, aber bei nicht-senkrechter Spiegelung weder winkel- noch längentreu. Sie sind flächentreue affine Abbildungen, aber im Allgemeinen keine Kongruenzabbildungen. Die gespiegelten geometrischen Figuren wirken bei nicht-senkrechter Spiegelung verzerrt. Die Bilder von Kreisen, Rechtecken und Quadraten unter einer Schrägspiegelung sind im Allgemeinen nicht wieder Kreise, Rechtecke und Quadrate, sondern Ellipsen und Parallelogramme. Schrägspiegelungen gibt es auch im dreidimensionalen Raum und in höherdimensionalen Räumen. Verkettung zweier Schrägspiegelungen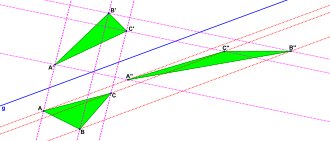 Die Verkettung zweier verschiedener Schrägspiegelungen an derselben Geraden g ist eine Scherung (Abbildung 2).[1] Weblinks
Einzelnachweise
|