|
ROC-KurveDie ROC-Kurve (ROC: englisch für receiver operating characteristic bzw. deutsch Operationscharakteristik eines Beobachters), auch Grenzwertoptimierungskurve oder Isosensitivitätskurve genannt ist eine Methode zur Bewertung und Optimierung von Analysestrategien. Die ROC-Kurve stellt visuell die Abhängigkeit der Effizienz mit der Fehlerrate für verschiedene Parameterwerte dar. Sie ist eine Anwendung der Signalentdeckungstheorie. Die ROC-Kurve kann eingesetzt werden, um den bestmöglichen Wert eines Parameters zu finden, beispielsweise bei einem dichotomen (semi-)quantitativen Merkmal oder Zwei-Klassen-Klassifizierungsproblem. Berechnung der ROC-Kurve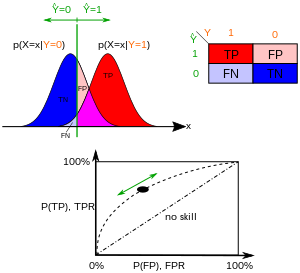 Für jeden möglichen Parameterwert (z. B. Sendegeschwindigkeit, Frequenz, …) ermittelt man die resultierenden relativen Häufigkeitsverteilungen in Form von Sensitivität (Richtig-Positiv-Rate) und Falsch-Positiv-Rate. In einem Diagramm trägt man Sensitivität (Richtig-Positiv-Rate) als Ordinate („-Achse“) und Falsch-Positiv-Rate als Abszisse („-Achse“) ein. Der Parameterwert selbst taucht dabei nicht auf, kann aber als Beschriftung der Punkte verwendet werden. Es resultiert typischerweise eine gekrümmte, aufsteigende Kurve. Interpretation der ROC-KurveDie ROC-Kurve ist ein Hilfsmittel zur Entscheidungsfindung, um möglicherweise optimale Modelle auszuwählen und suboptimale Modelle zu verwerfen. Je näher die ROC-Kurve an der oberen linken Ecke liegt, desto besser ist die Leistung des Modells. Eine ROC-Kurve nahe der Diagonalen deutet auf einen Zufallsprozess hin: Werte nahe der Diagonalen bedeuten eine gleiche Trefferquote und Falschpositivquote, was der zu erwartenden Trefferhäufigkeit eines Zufallsprozesses entspricht. Die ideale ROC-Kurve steigt zunächst senkrecht an (die Trefferquote liegt nahe bei 100 %, während die Fehlerquote anfangs noch nahe bei 0 % bleibt), erst danach steigt die Falsch-Positiv-Rate an. Eine ROC-Kurve, die deutlich unterhalb der Diagonalen bleibt, deutet darauf hin, dass die Werte falsch interpretiert wurden. Anwendung als OptimierungsmethodeDas theoretische Optimum (im Sinne eines Kompromisses aus Treffer- und Fehlerrate) des getesteten Wertes ermittelt man visuell dann aus dem Kontaktpunkt einer 45° ansteigenden Tangente mit der ROC-Kurve, sofern die Achsen einheitlich skaliert wurden. Andernfalls muss der Tangentenanstieg gleich dem der Diagonalen sein. Zeichnet man die Testwerte (beispielsweise in Abhängigkeit von der Falsch-Positiv-Rate) in das gleiche Diagramm, findet sich der Grenzwert als Lot des Kontaktpunktes der Tangente auf die Testwertekurve. Alternativ können die Punkte der Kurve mit dem Testwert beschriftet werden. Rechnerisch sucht man den Testwert mit dem höchsten Youden-Index. Dieser berechnet sich aus (mit relativen Werten berechnet). Eine alternative Methode, die vor allem im Information Retrieval Anwendung findet, ist die Betrachtung von Recall und Precision. Anwendung als QualitätsmaßEine ROC-Kurve kann auch als Qualitätsmaß verwendet werden. Dies ist oft im Bereich des Information Retrieval der Fall. Um unabhängig vom Testwert bewerten zu können, wird die ROC-Kurve für alle oder eine Stichprobe von Testwerten berechnet. Zu der ROC-Kurve berechnet man die Fläche unter der Grenzwertoptimierungskurve bzw. Fläche unter der ROC-Kurve (kurz, AUROC). Dieser Wert kann zwischen 0 und 1 liegen, wobei aber 0,5 der schlechteste Wert ist. Wie zuvor beschrieben, ist eine ROC-Kurve nahe der Diagonalen das zu erwartende Ergebnis eines Zufallsprozesses, der eine Fläche von 0,5 hat. Die zuvor als optimal beschriebene Kurve hat eine Fläche zwischen 0,5 und 1. Die Kurve mit der Fläche kleiner 0,5 kann in der Informationstheorie aber letztlich genauso gut sein, wenn man das Ergebnis entsprechend umgekehrt interpretiert („positiv“ und „negativ“ vertauscht). Der entscheidende Vorteil der Verwendung der Fläche unter der Grenzwertoptimierungskurve gegenüber beispielsweise der reinen Fehlklassifikationsrate ist, dass hier der Parameterwert entfällt, während letztere immer nur für einen einzelnen konkreten Parameterwert berechnet werden kann. Ein hoher AUROC-Wert bedeutet anschaulich „für geeignete Wahl des Parameters ist das Ergebnis gut“. BeispielIm Information Retrieval kann hier beispielsweise die Qualität eines Suchergebnisses bewertet werden. „Positiv“ ist hierbei ein passendes Suchergebnis, „Negativ“ ein unpassendes. Der Testwert ist die Anzahl der angeforderten Suchergebnisse. Enthält die Datenbank 10 relevante und 90 irrelevante Dokumente, und ein Verfahren hat in den ersten 12 Ergebnissen 7 relevante gefunden, so geht die ROC-Kurve durch den Punkt . Dies berechnet man für alle möglichen Anzahlen von Ergebnissen (0–100). Die Problemstellung als Optimierungsproblem wäre: „Was ist die optimale Anzahl von Ergebnissen, die ich betrachten sollte?“ Die Problemstellung als Qualitätsmaß wäre: „Unabhängig davon, wie viele Ergebnisse ich bekommen will, wie gut ist die Suchfunktion?“ In diesem Beispiel sind natürlich beide Fragestellungen nur bedingt sinnvoll. Intuition im maschinellen LernenIm maschinellen Lernen werden ROC-Kurven zur Evaluation der Klassifikatorperformance eingesetzt. Dabei wird die Fehlklassifikationsrate für eine größer werdende Menge von Instanzen bestimmt, angefangen bei den Instanzen, für die der Klassifikator am sichersten ist (weil sie zum Beispiel den größten Abstand zur Trennfunktion einer Support Vector Machine haben). Beispielhaft kann man sich einen Prüfer vorstellen, der den Prüfling die Fragen, bei denen dieser sich am sichersten fühlt, zuerst beantworten lässt. Im Verlauf der Prüfung kann der Prüfer eine ROC-Kurve erstellen. Gute Prüflinge geben dann erst zum Ende der Prüfung falsche Antworten, was sich aus der ROC-Kurve einfach ablesen lässt. Anwendung in der MedizinIn der Medizin ist die ROC-Kurve ein wichtiges Instrument zur Bewertung der Leistung von diagnostischen Tests. Sie wird häufig bei der Bewertung von medizinischen Screening-Verfahren eingesetzt. Die ROC-Kurve wird eingesetzt, um festzustellen, wie gut ein medizinischer Test zwischen erkrankten und nicht erkrankten Zuständen unterscheiden kann. ROC-Kurven werden in verschiedenen medizinischen Bereichen, einschließlich der Radiologie und der Labormedizin, häufig zur Bewertung der diagnostischen Genauigkeit von Tests, verwendet. Beispiel: Eine häufige Anwendung ist die Krebsdiagnose, bei der ein Test den Gehalt eines Biomarkers im Blut messen kann. Indem sie den Schwellenwert für ein positives Testergebnis variieren, können Ärzte mithilfe von ROC-Kurven beurteilen, wie gut der Test zwischen Patienten mit und ohne Krebs unterscheidet. Anwendung in der MeteorologieWird bei der Überprüfung von Wetter-Prognosemodellen in der Meteorologie verwendet. In der Meteorologie werden ROC-Kurven zur Bewertung der Qualität von Vorhersagen verwendet, insbesondere für binäre Ergebnisse wie das Eintreten eines Wetterereignisses. Die ROC-Kurve stellt die Trefferquote (Entdeckungswahrscheinlichkeit) gegen die Falschalarmquote dar, wenn die Entscheidungsschwelle variiert. Meteorologen nutzen die ROC-Analyse, um die Leistung verschiedener Vorhersagemodelle zu bewerten und den wirtschaftlichen Wert von Vorhersagesystemen zu verstehen. In der Meteorologie werden ROC-Kurven zur Bewertung der Qualität von Vorhersagen verwendet, insbesondere für binäre Ereignisse wie das Auftreten oder Nichteintreten eines bestimmten Wetterereignisses (z. B. Regen oder Frost). So kann eine Wettervorhersage beispielsweise Frost auf der Grundlage von Temperaturschwellen vorhersagen. Durch Variation dieser Schwellenwerte können Meteorologen die ROC-Kurve aufzeichnen, um zu veranschaulichen, wie gut das Vorhersagesystem zwischen Frost und keinem Frost unterscheidet. Die ROC-Kurve hilft so bei der Ermittlung der Kompromisse zwischen der Erkennung echter Ereignisse und der Minimierung von Fehlalarmen, was für eine effektive Wettervorhersage entscheidend ist. Siehe auchLiteratur
|



