Mealy-Automat

Ein Mealy-Automat ist in der theoretischen Informatik ein deterministischer endlicher Automat, dessen Ausgabe von seinem Zustand und seiner Eingabe abhängt; in der Veranschaulichung wird jeder Kante im Zustandsdiagramm ein Ausgabewert zugeordnet. Der Name geht auf den Mathematiker George H. Mealy zurück.

Formale Definition

Ein Mealy-Automat kann als 7-Tupel ${\displaystyle {\mathcal {A}}=\left(Q,\Sigma ,\Omega ,\delta ,\lambda ,q_{0},F\right)}$ definiert werden:

1. ${\displaystyle Q}$ ist eine endliche Menge von Zuständen (${\displaystyle \left|Q\right|<\infty }$). Statt ${\displaystyle Q}$ wird oft auch ${\displaystyle Z}$ verwendet.
2. ${\displaystyle \Sigma }$ ist das Eingabealphabet, ${\displaystyle \left|\Sigma \right|<\infty }$.
3. ${\displaystyle \Omega }$ ist das Ausgabealphabet, ${\displaystyle \left|\Omega \right|<\infty }$.
4. ${\displaystyle \delta \colon Q\times \Sigma \rightarrow Q}$ ist die Übergangsfunktion.
5. ${\displaystyle \lambda \colon Q\times \Sigma \rightarrow \Omega }$ ist die Ausgabefunktion.
   Gelegentlich wird eine kompaktere Notation gewählt und beide Funktionen zu einer Zustandsübergangsfunktion ${\displaystyle \zeta \colon Q\times \Sigma \rightarrow \Omega \times Q}$ zusammengefasst.
6. ${\displaystyle q_{0}\in Q}$ ist der Startzustand. Statt ${\displaystyle q_{0}}$ wird oft auch ${\displaystyle z_{0}}$ oder ${\displaystyle S_{0}}$ verwendet. Dieser Startzustand wird mit einer doppelten Umrandung bzw. einem Doppelpfeil gekennzeichnet.
7. ${\displaystyle F\subseteq Q}$ ist eine (endliche) Menge möglicher akzeptierender Zustände (= Endzustandsmenge).

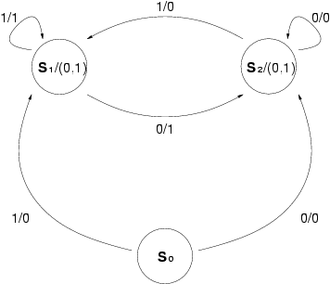
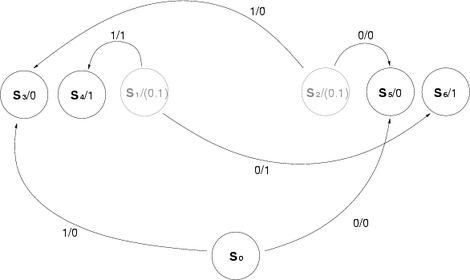
Wenn die reguläre Sprache des Automaten uninteressant ist, kann diese auch weggelassen werden. Dann wird der Automat als 6-Tupel definiert.

Beispiel

Der durch das folgende Zustandsdiagramm beschriebene Automat gibt seine Eingabe verzögert aus, d. h. zu einer Eingabe x₀x₁...x_n erzeugt er die Ausgabe 0x₀x₁...x_n-1. Hierbei bedeutet die Kantenbeschriftung 0/1, dass bei Eingabe einer Null zusätzlich zum Wechsel des Zustands eine Eins ausgegeben wird. S bezeichnet den jeweiligen Zustand.

Zusammenhang mit Moore-Automat

Die Ausgabe eines Moore-Automaten hängt im Gegensatz zum Mealy-Automaten nicht von seiner Eingabe ab. Mealy- und Moore-Automaten lassen sich ineinander umwandeln. Will man beispielsweise einen Mealy-Automaten in einen Moore-Automaten umwandeln, kann man in folgenden drei Schritten vorgehen:

Schritt 1: Ausgabe in die Knoten schreiben

Für jede Kante wird die Ausgabe in den Zustand übertragen, auf dem die Kante endet. Hierbei stehen in der Regel verschiedene Ausgabewerte in einem Zustandsknoten.

Schritt 2: Knoten aufspalten und eingehende Kanten umhängen

Die Zustände werden vervielfacht, so dass jedem Zustand nur noch höchstens ein Ausgabewert zugeordnet ist; anschließend hängt man eingehende Kanten entsprechend der Ausgabewerte auf die neuen Zustände um.

Schritt 3: Ausgehende Kanten vervielfachen

Zuletzt muss man alle ausgehenden Kanten der ursprünglichen Zustände kopieren und an die Zustände aus Schritt 2 anhängen.

Die Ausgabe des so konstruierten Moore-Automaten ist äquivalent zu der des ursprünglichen Mealy-Automaten.

Literatur

• G. H. Mealy: A Method for Synthesizing Sequential Circuits, Bell System Tech. J. 34, pp. 1045–1079, September 1955.
• Fricke, Digitaltechnik, Kapitel 8 "Synchrone Schaltwerke" bis inklusive 8.4. ISBN 978-3-8348-1783-9
• Reichardt, Lehrbuch Digitaltechnik, Kapitel 12 "Entwurf synchroner Zustandsautomaten". ISBN 978-3-11-047800-6