Lydersen-Methode

Die Lydersen-Methode[1] ist eine Gruppenbeitragsmethode zur Abschätzung der kritischen Größen ${\displaystyle T_{\text{c}}}$, ${\displaystyle P_{\text{c}}}$ und ${\displaystyle V_{\text{c}}}$. Die Lydersen-Methode ist Vorbild für viele neuere Modelle nach Joback[2], Ambrose[3], Constantinou und Gani[4] u. a. Die Lydersen-Methode basiert im Falle der Abschätzung der kritischen Temperatur auf der Guldberg-Regel, welche die kritische Temperatur in ein Verhältnis zum Normalsiedepunkt setzt.

Bestimmungsgleichungen

• Kritische Temperatur:

  ${\displaystyle T_{\text{c}}={\frac {T_{\text{b}}}{0{,}567+\sum G_{\text{i}}-\left(\sum G_{\text{i}}\right)^{2}}}}$

• Kritischer Druck:

  ${\displaystyle P_{\text{c}}={\frac {M}{\left(0{,}34+\sum G_{\text{i}}\right)^{2}}}}$

• Kritisches Volumen:

  ${\displaystyle V_{\text{c}}=40+\sum G_{\text{i}}}$

${\displaystyle T_{\text{b}}}$ ist der Normalsiedepunkt, ${\displaystyle M}$ die molare Masse, ${\displaystyle G_{\text{i}}}$ sind Gruppenbeiträge (unterschiedlich für die einzelnen Größen) für funktionelle Gruppen eines Moleküls.

Gruppenbeiträge

Gruppe	Gi (Tc)	Gi (Pc)	Gi (Vc)		Gruppe	Gi (Tc)	Gi (Pc)	Gi (Vc)
–CH3,–CH2–	0,020	0,227	55,0		>CH	0,012	0,210	51,0
–C<	—	0,210	41,0		=CH2,=CH	0,018	0,198	45,0
=C<,=C=	—	0,198	36,0		=C–H,=C–	0,005	0,153	36,0
–CH2–(Ring)	0,013	0,184	44,5		>CH– (Ring)	0,012	0,192	46,0
>C< (Ring)	−0,007	0,154	31,0		=CH–,=C<,=C=(Ring)	0,011	0,154	37,0
–F	0,018	0,224	18,0		–Cl	0,017	0,320	49,0
–Br	0,010	0,500	70,0		–I	0,012	0,830	95,0
–OH	0,082	0,060	18,0		–OH(Aromat)	0,031	−0,020	3,0
–O–	0,021	0,160	20,0		–O– (Ring)	0,014	0,120	8,0
>C=O	0,040	0,290	60,0		>C=O (Ring)	0,033	0,200	50,0
HC=O–	0,048	0,330	73,0		–COOH	0,085	0,400	80,0
-COO-	0,047	0,470	80,0		-NH2	0,031	0,095	28,0
>NH	0,031	0,135	37,0		>NH(Ring)	0,024	0,090	27,0
>N	0,014	0,170	42,0		>N–(Ring)	0,007	0,130	32,0
–CN	0,060	0,360	80,0		-NO2	0,055	0,420	78,0
–SH,–S–	0,015	0,270	55,0		–S– (Ring)	0,008	0,240	45,0
=S	0,003	0,240	47,0		>Si<	0,030	0,540	—
–B<	0,030	—	—

Beispielrechnung

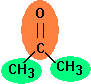
Aceton wird in zwei unterschiedliche Fragmente zerlegt, eine Carbonylgruppe und zwei Methylgruppen. Für das kritische Volumen ergibt sich folgende Rechnung:

${\displaystyle V_{\text{c}}=40+60{,}0+2\cdot 55{,}0=210~\mathrm {cm^{3}} }$

In der Literatur[5] finden sich Werte von 215,90 cm^3,[6] 230,5 cm^3[7] und 209,0 cm^3.[8]

Einzelnachweise

1. Lydersen a.L., „Estimation of Critical Properties of Organic Compounds“, University of wisconsin College Engineering, Eng. Exp. Stn. Rep. 3, Madison, Wisconsin
2. K. G Joback, R. C Reid: Estimation of pure-component properties from group-contributions. In: Chemical Engineering Communications. Band 57, Nr. 1, 1987, S. 233–243. 
3. D. Ambrose, Teddington (England). Div. of Chemical Standards National Physical Lab.: Correlation and estimation of vapour-liquid critical properties. Part 1: Critical temperatures of organic compounds. Rep.No. 92. National Physical Lab., Teddington (England). Div. of Chemical Standards, 1978, S. 1–35. 
4. Leonidas Constantinou, Rafiqul Gani: New group contribution method for estimating properties of pure compounds. In: AIChE Journal. Band 40, Nr. 10, Oktober 1994, S. 1697–1710, doi:10.1002/aic.690401011. 
5. Dortmunder Datenbank
6. A. N. Campbell, R. M. Chatterjee: The critical constants and orthobaric densities of acetone, chloroform, benzene, and carbon tetrachloride. In: Canadian Journal of Chemistry. Band 47, Nr. 20, 15. Oktober 1969, S. 3893–3898, doi:10.1139/v69-646. 
7. W. Herz, E. Neukirch: On Knowledge of the Critical State. In: Z.Phys.Chem.(Leipzig). Band 104, 1923, S. 433–450. 
8. Kenneth A. Kobe, Horace R. Crawford, Robert W. Stephenson: Industrial Design Data – Critical Properties and Vapor Presesures of Some Ketones. In: Industrial & Engineering Chemistry. Band 47, Nr. 9, September 1955, S. 1767–1772, doi:10.1021/ie50549a025.