Lowest Common Ancestor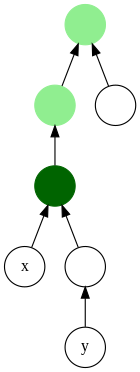

In diesem Baum ist der LCA der Knoten x und y in Dunkelgrün mar­kiert. Andere ge­mein­same Vorfahren sind in Hellgrün dar­ge­stellt.

Als Lowest Common Ancestor oder Least Common Ancestor (LCA), deutsch „letzter gemeinsamer Vorfahre“, wird in der Informatik und Graphentheorie ein Ermittlungskonzept bezeichnet, das einen gegebenen gewurzelten Baum von Datenstrukturen effizient vor­ver­arbei­tet, sodass anschließend Anfragen nach dem letzten gemeinsamen Vorfahren für beliebige Knotenpaare in konstanter Zeit beantwortet werden können.

Bäume gehören zu den fundamentalen Datenstrukturen der Informatik. Sie werden häufig verwendet, um Daten in einer hierarchischen oder geschachtelten Struktur darzustellen. Zwei klassische Beispiele sind Such- und Entscheidungsbäume. Algorithmische Standard­fragen für Bäume sind zum Beispiel die Pre-, Post- und Inordertraversierung. Ein in diesem Kontext weniger bekanntes algorithmisches Problem ist die Suche nach dem letzten ge­mein­samen Vorfahren (LCA).[1]

Definition des LCA

Gegeben sei ein Baum ${\displaystyle T=(V,E)}$ mit einem Wurzelknoten ${\displaystyle r}$, insgesamt ${\displaystyle n}$ Knoten ${\displaystyle (|V|=n)}$ und einer Höhe ${\displaystyle h}$. Der Lowest Common Ancestor (LCA) zweier Knoten ${\displaystyle u}$ und ${\displaystyle v}$ ist derjenige Knoten, der ein Elternknoten von sowohl ${\displaystyle u}$ als auch ${\displaystyle v}$ ist und am weitesten von der Wurzel ${\displaystyle r}$ entfernt liegt, also die größtmögliche Tiefe besitzt.

Ziel ist es, einen gegebenen Baum ${\displaystyle T}$ effizient so vorzuverarbeiten, dass LCA ${\displaystyle (u,v)}$ Anfragen möglichst schnell beantwortet werden können.

Entwicklung (Geschichte)

Das LCA-Problem wurde 1973 erstmals von Alfred Aho, John Hopcroft und Jeffrey Ullman definiert.

Im Jahre 1984 entwickelten Dov Harel und Robert Tarjan die erste effiziente Datenstruktur zur Lösung des LCA-Problems. Dabei wird der Eingabebaum in ${\displaystyle {\mathcal {O}}(n)}$ (siehe Landau-Symbole) vorverarbeitet, so dass die Abfragen in konstanter Zeit, ${\displaystyle {\mathcal {O}}(1)}$ beantwortet werden können. Allerdings gilt die Datenstruktur als sehr komplex und schwierig zu implementieren. Tarjan fand später einen einfacheren, wenn auch weniger effizienten Algorithmus, der auf der Union-Find-Struktur basiert und den LCA aus einer vorher berechneten Menge von Knotenpaaren ermittelt (Tarjan’s Offline Least Common Ancestor Algorithm (TOLCA)). Im Jahre 1988 vereinfachten Baruch Schieber und Uzi Vishkin diese Datenstruktur, so dass diese implementierbar wurde und dennoch einen Vorverarbeitungsaufwand von ${\displaystyle {\mathcal {O}}(n)}$ Zeit und einen Abfrageaufwand von ${\displaystyle {\mathcal {O}}(1)}$ aufweist.

1993 entdeckten Omer Berkman und Uzi Vishkin einen neuen Weg, das LCA-Problem mit Hilfe von Reduktion und Range Minimum Query (RMQ) zu lösen. Der Zeitaufwand hat auch hier lineare Vorverarbeitungszeit ${\displaystyle {\mathcal {O}}(n)}$ und konstante Abfragezeit ${\displaystyle {\mathcal {O}}(1)}$. Dieser Lösungsansatz wurde 2000 von Michael Bender und Martin Farach-Colton vereinfacht.[2][3]

Anwendungsgebiete

Die LCA-Ermittlung kann angewendet werden, um den LCA (Last common ancestor, auch Most recent common ancestor, MRCA) von Gen-Bäumen (Bioinformatik) zu ermitteln.[4]

Verallgemeinerung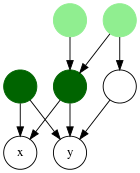

Ein gerichteter azyk­lischer Graph mit den ge­mein­samen Vorfahren von x und y in Hell­grün und ihren LCAs in Dun­gkel­ggrün.

Ursprünglich wurde der Begriff des LCA im Zusammenhang mit Bäumen untersucht, doch kann er auch für gerichtete azyk­lische Graphen (englisch directed acyclic graphs, DAGs) definiert werden. Dabei wird davon ausgegangen, dass die Kanten des DAG von den Eltern zu den Kindern führen. Die ursprüngliche Definition von Aït-Kaci et al. (1989)[5] wurde von Bender et al. (2005) vereinfacht.[6]

Weblinks

• Ermittlung des Lowest Common Ancestors mithilfe des RMQ-Algorithmus

Einzelnachweise

1. Effiziente Berechnung vom letzten ge­mein­samen Vorfahren und Anwendungen – FU Berlin. Auf: fu-berlin.de – abgerufen am 22. Januar 2023
2. Michael A. Bender, Martin Farach-Colton: The LCA problem revisited. In: Proceedings of the 4th Latin American Symposium on Theoretical Informatics. Serie: Lecture Notes in Computer Science, Band 1776, Springer-Verlag, 2000, ISBN 978-3-540-67306-4, S. 88–94; doi:10.1007/10719839_9 (englisch).
3. Algorithmen zum Ermitteln des Lowest Common Ancestor (LCA) – FU Berlin (PDF, 638 kB) fu-berlin.de – abgerufen am 10. März 2013
4. Jana Hertel, Peter F. Stadler: BIOINF 15-037: The Expansion of Animal MicroRNA Families Revisited. In: bioinf.uni-leipzig.de. Bioinformatics Leipzig, abgerufen am 22. Januar 2023 (englisch). 
5. H. Aït-Kaci, R. Boyer, P. Lincoln, R. Nasr: Efficient implementation of lattice operations. In: ACM Transactions on Programming Languages and Systems. 11. Jahrgang, Nr. 1, 1989, S. 115–146, doi:10.1145/59287.59293 (englisch). 
6. Michael A. Bender, Martín Farach-Colton, Giridhar Pemmasani, Steven Skiena, Pavel Sumazin: Lowest common ancestors in trees and directed acyclic graphs. In: Journal of Algorithms. 57. Jahrgang, Nr. 2, 2005, S. 75–94, doi:10.1016/j.jalgor.2005.08.001 (englisch).