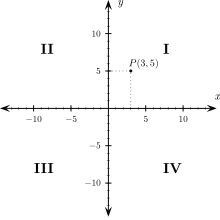
Die Koordinatenebene im zweidimensionalen Raum Als Koordinatenebene bezeichnet man in der analytischen Geometrie eine von zwei Einheitsvektoren aufgespannte Ursprungsebene . In zwei Dimensionen entspricht die Koordinatenebene der euklidischen Ebene und damit der Grundfläche eines kartesischen Koordinatensystems . Im dreidimensionalen Raum gibt es drei Koordinatenebenen: die xy-Ebene , die xz-Ebene und die yz-Ebene .
Analytische Geometrie
Bezeichnungen
Die drei Koordinatenebenen im dreidimensionalen Raum Im Folgenden seien die drei Koordinatenachsen des dreidimensionalen Raums
R
3
{\displaystyle \mathbb {R} ^{3}}
x
1
{\displaystyle x_{1}}
x
2
{\displaystyle x_{2}}
x
3
{\displaystyle x_{3}}
E
{\displaystyle E}
Einheitsvektoren angeben, von denen die Ebene aufgespannt wird:
die
x
1
x
2
{\displaystyle x_{1}x_{2}}
E
12
{\displaystyle E_{12}}
e
→
1
{\displaystyle {\vec {e}}_{1}}
e
→
2
{\displaystyle {\vec {e}}_{2}}
die
x
1
x
3
{\displaystyle x_{1}x_{3}}
E
13
{\displaystyle E_{13}}
e
→
1
{\displaystyle {\vec {e}}_{1}}
e
→
3
{\displaystyle {\vec {e}}_{3}}
die
x
2
x
3
{\displaystyle x_{2}x_{3}}
E
23
{\displaystyle E_{23}}
e
→
2
{\displaystyle {\vec {e}}_{2}}
e
→
3
{\displaystyle {\vec {e}}_{3}}
Hierbei sind die drei Einheitsvektoren
e
→
1
=
(
1
,
0
,
0
)
{\displaystyle {\vec {e}}_{1}=(1,0,0)}
e
→
2
=
(
0
,
1
,
0
)
{\displaystyle {\vec {e}}_{2}=(0,1,0)}
e
→
3
=
(
0
,
0
,
1
)
{\displaystyle {\vec {e}}_{3}=(0,0,1)}
Oktanten zerlegt. Der Schnitt zweier Koordinatenebenen ergibt eine Koordinatenachse, der Schnitt aller drei Koordinatenebenen den Koordinatenursprung .
Ebenengleichungen
Die drei Koordinatenebenen werden durch die folgenden Ebenengleichungen charakterisiert:
Koordinatenebene
Koordinatenform
Normalenform
Parameterform
Achsenabschnittsform
E
12
{\displaystyle E_{12}}
x
3
=
0
{\displaystyle x_{3}=0}
e
→
3
⋅
x
→
=
0
{\displaystyle {\vec {e}}_{3}\cdot {\vec {x}}=0}
x
→
=
s
e
→
1
+
t
e
→
2
{\displaystyle {\vec {x}}=s\,{\vec {e}}_{1}+t\,{\vec {e}}_{2}}
nicht definiert
E
13
{\displaystyle E_{13}}
x
2
=
0
{\displaystyle x_{2}=0}
e
→
2
⋅
x
→
=
0
{\displaystyle {\vec {e}}_{2}\cdot {\vec {x}}=0}
x
→
=
s
e
→
1
+
t
e
→
3
{\displaystyle {\vec {x}}=s\,{\vec {e}}_{1}+t\,{\vec {e}}_{3}}
nicht definiert
E
23
{\displaystyle E_{23}}
x
1
=
0
{\displaystyle x_{1}=0}
e
→
1
⋅
x
→
=
0
{\displaystyle {\vec {e}}_{1}\cdot {\vec {x}}=0}
x
→
=
s
e
→
2
+
t
e
→
3
{\displaystyle {\vec {x}}=s\,{\vec {e}}_{2}+t\,{\vec {e}}_{3}}
nicht definiert
Hierbei sind
x
→
=
(
x
1
,
x
2
,
x
3
)
∈
R
3
{\displaystyle {\vec {x}}=(x_{1},x_{2},x_{3})\in \mathbb {R} ^{3}}
x
→
⋅
y
→
{\displaystyle {\vec {x}}\cdot {\vec {y}}}
Skalarprodukt der Vektoren
x
→
{\displaystyle {\vec {x}}}
y
→
{\displaystyle {\vec {y}}}
s
{\displaystyle s}
t
{\displaystyle t}
Darstellende Geometrie
In der darstellenden Geometrie entsprechen die drei Koordinatenebenen häufig der Grundrissebene, der Aufrissebene und der Kreuzrissebene.
Synthetische Geometrie
In der synthetischen Geometrie wird eine affine oder projektive Ebene , der als Koordinatenbereich eine Menge mit einer bestimmten algebraischen Struktur (ein Ternärkörper , Quasikörper , Alternativkörper , Schiefkörper etc.) zugeordnet werden kann, als Koordinatenebene über diesem verallgemeinerten Körper bezeichnet.
Literatur
Wolf-Dieter Klix, Karla Nestler: Konstruktive Geometrie . Hanser, 2001, ISBN 3-446-21566-2 .
Max Koecher, Aloys Krieg: Ebene Geometrie . 3. Auflage. Springer, 2007, ISBN 3-540-49328-X .
Weblinks