|
Isotonische Regression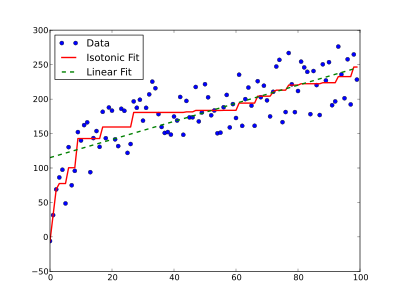 Die isotonische Regression ist ein Regressionsverfahren, mit dem eine isotone (ordnungserhaltende) Abbildung zwischen einer abhängigen und einer unabhängigen Variable gefunden wird. Werden monotone Abbildungen, also isotone sowie antitone Abbildungen, betrachtet, bezeichnet man das Verfahren als monotone Regression. Die von der Abbildung beschriebene Kurve hat anders als beispielsweise die lineare Regression keine feste Form, sondern nur die Beschränkung, monoton steigend (oder fallend) zu sein, während die Entfernung zu den Datenpunkten so gering wie möglich ist. AnwendungWird zwischen einem Parameter und Messwerten eines Experiments eine monotone Beziehung erwartet, kann diese durch monotone Regression bestimmt werden, auch wenn die Messwerte durch Rauschen verfälscht sind. Eine Modellannahme wie Linearität muss dabei nicht getätigt werden. Im Bereich des maschinellen Lernens finden sich oft Modelle, die eine Wahrscheinlichkeit für eine Klassifikation von Datenpunkten ausgeben. Je nach Modellart können die vorhergesagten Wahrscheinlichkeiten im Vergleich zur Häufigkeit der Klassen in den Daten verzerrt sein. Zur Korrektur können die Vorhersagen kalibriert werden. Eine dafür geeignete Methode basiert auf isotonischer Regression.[1] AlgorithmusBei der isotonischen Regression erfolgt eine Anpassung von Werten an Beobachtungen mit zugehörigen Gewichten mithilfe der Methode der kleinsten Quadrate, wobei Nebenbedingungen der Form (meist ) eingehalten werden müssen. Das heißt, jeder Punkt muss einen mindestens so hohen Wert wie der vorherige Punkt haben. Die Bedingungen beschreiben eine partielle oder totale Ordnung, die als gerichteter Graph definiert werden kann, wobei die Menge der Beobachtungen und die Menge der Paare bezeichnet, für die gilt. Damit kann die isotonische Regression als folgendes quadratisches Programm formuliert werden: Wenn eine totale Ordnung ist, kann das Problem in gelöst werden.[2] Einzelnachweise
|











