Gibbssches Phänomen

Als Gibbs’sches Phänomen bezeichnet man in der Mathematik das Verhalten, dass bei abgebrochenen Fourierreihen und bei der Fourier-Transformation von stückweise stetigen, differenzierbaren Funktionen in der Umgebung von Sprungstellen sogenannte Überschwingungen auftreten. Diese Überschwingungen verschwinden auch dann nicht, wenn die endliche Anzahl von Termen zur Approximierung bzw. die Bandbreite auf beliebig hohe, aber endliche Werte erhöht wird, sondern weisen in der maximalen Auslenkung eine konstante, relative Auslenkung von ca. 9 % auf.[1]

Der Effekt wurde nach dem amerikanischen Physiker Josiah Willard Gibbs benannt, der sich um 1898 mit der Analyse von Kippschwingungen beschäftigte. Die Bezeichnung stammt von dem Mathematiker Maxime Bôcher, der 1906 die praktisch motivierten Arbeiten von Gibbs mathematisch korrekt ausformulierte. Erste Arbeiten zu dem Effekt datieren allerdings auf den 50 Jahre früher tätigen englischen Mathematiker Henry Wilbraham (1825–1883), dessen 1848 publizierte Arbeit zu der Zeit aber keine weitere Beachtung fand.[2]

Das Gibbs’sche Phänomen ist im Bereich der Signalverarbeitung einer von mehreren Effekten, die auch als Ringing bezeichnet werden.[3] Das spezifische Gibbs’sche Phänomen sollte nicht mit dem allgemeinen Überschwingen von Signalen verwechselt werden.

Beschreibung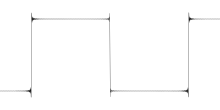

Gibbssches Phänomen bei einem periodischen Rechtecksignal, mit 5 Oberschwingungen approximiert

Rechtecksignal mit 25 Oberschwingungen approximiert

Rechtecksignal mit 125 Oberschwingungen approximiert

Entwickelt man eine Fourierreihe einer unstetigen, periodischen Funktion, wie beispielsweise der Rechteckfunktion, so ergeben sich an den Unstetigkeitsstellen typische Über- und Unterschwinger, die sich auch dann nicht verringern, wenn man versucht, die Funktion durch weitere Summenglieder anzunähern wie in den Darstellungen mit 5, 25 und 125 Oberschwingungen demonstriert. Dabei ist erkennbar, dass zwar die Frequenz der Überschwingung zunimmt und die Dauer abnimmt, die maximale Auslenkung der Überschwingung kurz vor bzw. nach der Sprungstelle bleibt aber konstant.

Analog tritt das Gibbs’sche Phänomen auch bei Fourier-Transformation an Sprungstellen auf, wobei dabei die zu approximierende Funktion nicht periodisch sein muss.

Physikalisch liegt die Bedeutung darin, dass jedes real existierende System auch die Eigenschaft eines Tiefpasses aufweist und ein Signal in seiner Bandbreite limitiert. Sprungstellen, die „unendlich viele“ Frequenzanteile aufweisen, können in realen Systemen nicht auftreten.

Berechnung

Die relative Höhe des Überschwingers in einer Richtung, bezogen auf die Sprunghöhe, lässt sich im Grenzwert unendlich vieler Fourier-Summenglieder bestimmen zu:

${\displaystyle {\frac {1}{\pi }}\int _{0}^{\pi }{\frac {\sin t}{t}}\,\mathrm {d} t-{\frac {1}{2}}\approx 0{,}08949}$ (Folge A243268 in OEIS),

womit sich ein prozentualer Fehler von etwa 9 % der Sprunghöhe ergibt. Der Integrand wird auch als Kardinalsinus oder als si-Funktion bezeichnet. Der Wert des Integrals

${\displaystyle \int _{0}^{\pi }{\frac {\sin t}{t}}\ \mathrm {d} t=(1{,}851937052\dots )={\frac {\pi }{2}}+\pi \cdot (0{,}089490\dots )}$ (Folge A036792 in OEIS)

wird als Wilbraham–Gibbs-Konstante bezeichnet.

Beispiel

Die Reihe mit ${\displaystyle n=50}$ Termen

${\displaystyle f(x)={\frac {\pi }{n}}[{\frac {\sin(x)}{1}}+{\frac {\sin(3x)}{3}}+{\frac {\sin(5x)}{5}}+\ldots }$

approximiert die Box-Funktion, -1 in ${\displaystyle [-\pi ,0]}$ und + 1 in ${\displaystyle [0,\pi ]}$. Die Ableitung ${\displaystyle f'(x)}$ hat den Wert ${\displaystyle 2n/\pi }$ im Punkt 0 und die erste Nullstelle (rechts vom Nullpunkt) liegt im Punkt ${\displaystyle \pi /n}$. In diesem Punkt hat ${\displaystyle f(x)}$ sein Maximum

${\displaystyle f(\pi /n)=\int _{0}^{\pi /n}f'(x)dx=1.18}$

Die Überschwingung liegt an dem etwas zu großen Wert von ${\displaystyle f'(x)}$ in der Mitte ${\displaystyle x=0}$ , denn wenn man von der Mitte aus, ${\displaystyle f(0)=0}$ , nach rechts geht, steigt ${\displaystyle f(x)}$ zunächst steil an und schießt über das Ziel 1 hinaus. Sobald aber die Oszillationen in ${\displaystyle f'(x)}$ beginnen sinkt ${\displaystyle f(x)}$ wieder, und das Integral ändert seinen Wert dann im Rhythmus der Hebungen und Senkungen von ${\displaystyle f'(x)}$ , behält aber eine mittlere Höhe von 1 bei. Ohne die Überschwingung würde ${\displaystyle f(x)}$ um einen tieferen Wert pendeln.

Rechtecksignal mit 50 Oberschwingungen approximiert

Der Flächeninhalt = ${\displaystyle 1/2\cdot 2n/\pi \cdot \pi /n=1}$ des mit ${\displaystyle n}$ immer steileren und schmaleren roten Dreiecks ist invariant und so behält auch die Überschwingung ihren Wert ${\displaystyle 1.18}$ bis zum Ende ${\displaystyle n\to \infty }$ durch.

Literatur

• Edwin Hewitt, Robert E. Hewitt: The Gibbs-Wilbraham phenomenon: An episode in fourier analysis. Archive History Exact Sciences, Band 21, 1979, S. 129–160.
• Fernando Puente León, Uwe Kiencke, Holger Jäkel: Signale und Systeme. 5. Auflage. Oldenbourg, 2011, ISBN 978-3-486-59748-6. 

Weblinks

• Eric W. Weisstein: Gibbs Phenomenon. In: MathWorld (englisch).

Einzelnachweise

1. H. S. Carslaw: Introduction to the theory of Fourier’s series and integrals. Third Edition Auflage. Dover Publications Inc., New York 1930, Chapter IX (Google Books). 
2. Edwin Hewitt, Robert E. Hewitt: The Gibbs-Wilbraham phenomenon: An episode in fourier analysis. In: Archive for History of Exact Sciences. Band 21, Nr. 2, 1979, S. 129–160, doi:10.1007/BF00330404. 
3. Eric W. Weisstein: Gibbs Phenomenon. In: MathWorld (englisch).