Detonationswelle

Sichtbare Detonationswelle (im Bild markiert) bei einer Explosion

Eine Detonationswelle ist die Stoßwelle, die sich aufgrund einer Explosion nach allen Seiten ausbreitet, falls die ursprüngliche Expansionsgeschwindigkeit größer ist als die Schallgeschwindigkeit im umgebenden Medium.

Voraussetzung für die schnelle Expansion ist eine erhöhte Schallgeschwindigkeit des explodierenden Materials, typischerweise in Verbindung mit hohen Temperaturen. So führt eine Dampfkesselexplosion zu einer Detonationswelle, das Bersten eines Druckluftbehälters dagegen nur zu einem Knall.

Allgemeines

‘Leise’ Schallwellen gehorchen der linearen Wellengleichung. Solche Schallwellen können sich gegenseitig ohne Wechselwirkung durchdringen. Die Kriterien für ‘leise’ (ohne Rücksicht auf das Trommelfell) sind, dass sowohl der Schalldruck als auch der Staudruck aufgrund der Schallschnelle klein sind im Vergleich zum statischen Druck. Unmittelbar einsichtige Gründe: Der Gesamtdruck darf nicht negativ werden und mit dem Druck steigt und fällt auch die Temperatur und damit die Schallgeschwindigkeit. Anschauliche Folge: Ein kurzer Wellenzug, der auf einem langen Wellenberg reitet, läuft schneller als dieser, bis er an die vordere Flanke gelangt. Ein noch kürzerer überlagert die beiden usw., sodass sich die Steilheit aller vorderen Flanken addiert.

Die Friedlander-Wellenform als Prototyp einer Detonationswelle.
Gezeigt ist die Differenz des Drucks zum statischen Druck, der 100 kPa beträgt (1 bar).

Friedlander hat 1946 die nebenstehend abgebildete Wellenform vorgeschlagen. Sie passt für nicht zu große Drücke gut zu experimentell ermittelten Druckverläufen.[1] Folgende Formel gibt diese Wellenform an als zeitlichen Druckverlauf an einem festen Raumpunkt:

${\displaystyle P(t)=P_{0}+P_{s}e^{-{\frac {t}{t^{*}}}}\left(1-{\frac {t}{t^{*}}}\right)\ }$ für t > 0, sonst ${\displaystyle P(t)=P_{0}\ .}$

Beschreibung: Ausgehend vom ungestörten, statischen Druck ${\displaystyle P_{0}}$ springt der Druck instantan auf ${\displaystyle P_{0}+P_{s}}$, um dann mit einem Unterschwingen (ab ${\displaystyle t=t^{*}}$) auf ${\displaystyle P_{0}}$ einzuschwingen.

Wilson-Wolke im Unterdruckbereich der Detonationswelle von 500 Tonnen TNT auf der Hawaii-Insel Kahoʻolawe.

Im Bereich ${\displaystyle P<P_{0}}$ kann die Temperatur unter den Taupunkt sinken und eine Wilson-Wolke entstehen, falls die Luftfeuchte ausreicht und der Abstand von einem ggf. nuklearen Feuerball groß genug ist.

Für höhere Drücke steigt die Temperatur so hoch, dass die Luft in Atome dissoziiert und ionisiert wird. Dadurch ändert sich erstens die Zustandsgleichung, zweitens entsteht viel Wärmestrahlung, die zusätzlich zur Wärmeleitung über die steile Stoßfront zur Dissipation der Energie in der Welle beiträgt. Bei Kernexplosionen liegt die thermische Strahlung im UV- und Röntgenbereich, wird also von Luft absorbiert, was die Berechnung der Detonationswelle verkompliziert.

Mit der Ausbreitung verteilt sich jedoch die Energie auf eine immer größere Oberfläche der Schockfront, bis die Welle in eine normale Schallwelle übergeht, die sich nur noch mit Schallgeschwindigkeit ausbreitet.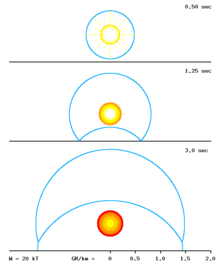

Abb. 2: Nichtlineare Reflexion der Druckwelle einer atomaren Luftexplosion

Ein wesentlich komplexeres Problem ist das Verhalten der Druckwelle unter Reflexion. Eine Explosion in der Nähe einer ebenen harten Fläche (z. B. Erdboden bei einer Luftexplosion, Abb. 2) führt zu einer Verstärkung der Druckwelle, die für unterschiedliche Abstände (Detonationshöhen) von der reflektierenden Fläche bei verschiedenen Druckwerten maximal wird. Das Verhältnis zwischen reflektierter Druckwelle und einfallender Druckwelle wird als Reflexionsfaktor bezeichnet. Das für Stoßwellen typische nichtlineare Verhalten bei Reflexionen wurde in den 1950er Jahren von den USA und der Sowjetunion in oberirdischen Kernwaffenversuchen ausführlich untersucht.

Ein Rechenmodell für atmosphärische Detonationswellen

Entfernungsabhängige Abnahme des Überdrucks (rot) und des dynamischen Drucks (gelb) einer Nuklearexplosion. Im steileren Bereich ist das Gas hoch ionisiert. Der Übergang der Stoßwelle zu einer normalen Schallwelle liegt außerhalb des Diagramms.

Die frühere US-Behörde Defense Nuclear Agency (DNA) hat um 1984 ein Modell zur rechnerischen Abschätzung von Explosionsdruckwellen entwickelt, welches die Abhängigkeit der Überdruckspitze als Funktion der Distanz sowie der Detonationshöhe und der Sprengenergie liefert. Obgleich das Modell ursprünglich für Nuklearexplosionen entwickelt wurde, kann es über Skalierungsregeln auch auf nahezu beliebige andere Explosionstypen angewendet werden, sofern die Explosion von einer Punktquelle ausgeht und Inhomogenitäten im umgebenden Medium oder der reflektierenden Oberfläche vernachlässigbar sind. Das Modell, das in Gestalt eines DOS-Programms BLAST vorliegt, unterliegt keiner Geheimhaltung. Es baut im Wesentlichen auf der Rankine-Hugoniot-Gleichung sowie empirischer Ausgleichungsrechnungen auf der Basis von Kernwaffentest-Daten auf.

Wirkungen

Druckdifferenz in mbar	Zerstörungswirkung[2]
2	Glasbruch weniger Fenster, die bereits unter Spannung stehen
3	Glasbruch durch Schalldruck von mehr als 140 dB
30	Leichte Schäden an Dächern; Glasbruch an 10 % der Fenster
30–100	Zerstörung von Fenstern; erste Schäden an Fensterrahmen
50	Kleine Schäden an Häusern
70	Teilweise Zerstörung von Häusern
70–140	Zerstörung von Wellblech und Holzwänden
70	Verletzungen durch umherfliegende Splitter
90–500	Schäden an Stahlkonstruktionen
140	Massive Schäden an Häusern und Dächern
140–200	Einsturz von Mauerwerk
160	Trommelfellruptur
170	Zerstörung von 50 % der Ziegelhäuser
200–280	Zerstörung von Stahlgerüsten
350–500	Nahezu vollständige Zerstörung von Gebäuden
480	Umwerfen von Autos
480–550	Versagen von 20 bis 30 cm dicken Ziegelwänden
620	Zerstörung von Autos
700	Vollständige Zerstörung von Gebäuden

Die Zar-Bombe verursachte die größte künstliche Druckwelle.

Siehe auch

• Machwelle

Literatur

• G. F. Kinney, K. J. Graham: Explosive shocks in air. Springer, Berlin/New York 1985, ISBN 3-540-15147-8.
• Arnold Berliner, Karl Scheel (Hrsg.): Physikalisches Handwörterbuch. Zweite Auflage, Verlag von Julius Springer, Berlin 1932.
• Wilhelm Jost: Explosions- und Verbrennungsvorgänge in Gasen. Verlag von Julius Springer, Berlin 1939.

Weblinks

Wikibooks: Formelsammlung Kernwaffenexplosion – Lern- und Lehrmaterialien

• Programm BLAST und andere
• Detonationswellen in engen Spalten (abgerufen am 13. Februar 2020)
• Wärmetransformationsprozesse ohne Phasenumwandlung (abgerufen am 14. Februar 2020)
• Effiziente numerische Simulation des Deflagrations–Detonations–Übergangs (abgerufen am 14. Februar 2020)
• Zur Detonationsphysik fester und flüssiger Sprengstoffe (abgerufen am 14. Februar 2020)

Einzelnachweise

1. J. M. Dewey: The shape of the blast wave: studies of the Friedlander equation. Presented at the 21st International Symposium on Military Aspects of Blast and Shock, Israel 2010 (Online).
2. PDF bei www.nrc.gov.