متحكم تناسبي تكاملي تفاضلي

آلية تحكم هوائي. تعد من أقدم أجهزة التحكم عن طريق PID. في أعلى الشكل يوجد ثلاثة عناصر قابلة للتحكم "% P" العنصر التناسبي بالنسبة، "J min" العنصر التكاملي بالدقائق، "D min" العنصر التفاضلي بالدقائق

حاكم أو متحكم بواسطة PID (بالإنجليزية: PID Controller)‏ هو حلقة تحكم شامل بتغذية رجعية شائع الاستخدام في نظم التحكم الصناعية.

PID هي اختصار Proportional + Integral + Derivative أي تناسبي + تكاملي + تفاضلي وهي المسؤولة عن تصحيح الخطأ الناتج عن الفرق بين القيمة المطلوبة والقيمة المقاسة.

شكل نموذجي لحاكم PID

يتمثل الخوارزم الحسابي لحاكم PID بثلاثة معاملات منفصلة: التناسب (P)، التكامل (I)، والتفاضل (D). القيمة التناسبية تبين رد الفعل مع الخطأ الحالي. القيمة التكاملية تتناسب مع استمرارية وجود الخطأ مع الزمن. القيمة التفاضلية تتناسب مع معدل التغير في الخطأ.

في الحقيقة ترتيب الاحرف أو الكلمات لا يعكس اسبقية العملية بالضرورة.

أساسيات حلقة التحكم

يمكن مشاهدة مثال حي لحلقة التحكم في حياتنا اليومية كما هو الحال في مرش الحمام حيث يمكن ضبط درجة الحرارة المناسبة يدويا. عندما نشعر بالبرودة فأننا سندير حنفية الماء الساخن لتفتح أكثر وربما العكس مع حنفية الماء البارد. تدعى عملية الشعور أو الإحساس (بتغير درجة الحرارة) بقياس قيمة العملية (Process Variable - PV) وتسمى درجة الحرارة المرغوبة بالقيمة المضبوطة (Set Point - SP) بينما يطلق على عملية التحكم بالصنبور أو الحنفية بالمتغير المتأثر (Manipulated Variable - MV). الأهم هنا هو من يقوم بعملية المعالجة وهو دماغ الإنسان. يمكن استبدال دماغ الإنسان بآلية تقوم بنفس الكيفية مثل تركيب جهاز لضبط الحرارة (ثرموستات مثلا أو خلاط حراري).

يمكن تلخيص حلقة التحكم بثلاثة وظائف أساسية هي:

• وظيفة القياس: تتم هذه الوظيفة بواسطة أجهزة تحسس أو مجسات وتدعى أحيانا بالمرسلات. من هذه المجسات مجس الحرارة، مجس الضغط، مجس الحركة، مجس التيار، مجس المقاومة، مجس التردد، وما إلى ذلك. يتم اختيار نوع المرسل وفقا للعملية المراد التحكم بها.
• وظيفة المقارنة والحساب: يتم مقارنة القيمة المقاسة عبر المرسل والقيمة المضبوطة مسبقا والتي يراد الوصول إليها. تسمى القيمة المقاسة PV بينما القيمة المضبوطة SP. نتيجة المقارنة ينشأ عنها قيمة تدعى الخطأ e، وتمرر بدوره إلى أحد أو مجموعة عناصر التحكم السابقة ونتيجة المعالجة أو الحساب ترسل إلى قسم التحكم النهائي للعمل بها.
• وظيفة التحكم النهائي: تختلف أنواع عناصر التحكم النهائي باختلاف العملية فهناك مثلا الصمامات لفتح وقفل الأنابيب، المحركات للتحكم بالسرعة والاتجاه، السخانات للتحكم بالحرارة وهكذا.

من ناحية أخرى يمكن تصنيف الوظائف حسب مبدأ عملها، يوجد ثلاثة أصناف هي:

• وظيفة العمل بضغط الهواءPneumatic air: يتم تمييز هذا النوع في الرسومات الصناعية بالخطوط المتواصلة _________.
• وظيفة العمل بضغظ السائل Hydraulic. يتم الرمز لهذا النوع بخطوط متصلة ولكن تقطعها حروف L أي ---L----L---
• وظيفة العمل بالتيار الكهربائي Electric current: يتم ترميز هذا النوع بخطوط متقطعة - - - - - - -.

التقنيات المتوفرة

• تقنية التحكم الهوائي PID Pneumatic Controller: وتعد من أوئل التقنيات التي تم تصنيعها لتطبيق نظرية التحكم بالعنصر التناسبي التكاملي التفاضلي.
• تقنية التحكم الإلكتروني Electronics PID Controller: وتعتمد بشكل رئيسي على المكبر العملياتي.
• تقنية التحكم الرقمي Digital Controller: وهي الأحدث والأكثر شيوعاً في الصناعة حيث تعتمد تقنيات تحكم متطورة قابلة للبرمجة والموالفة الذاتية.

نظرية التحكم نوع PID

يوجد ثلاثة أنواع رئيسية من نمط التحكم PID هي:

• النوع التسلسي أو المتفاعل Series PID: وفيه تكون عناصر أو حدود I و D مرتكز تماما على الحد P, بمعنى أنها لا تعمل بدونه.
• النوع المتفرع أو المستقل Parallel PID: تؤدى الوظائف P، I، وD بشكل مستقل عن بعضها ثم تجمع معا إلى خرج واحد.
• النوع المختلط Mixed PID: وهو مزيج من التسلسلي والمتوازي.

كما أن الأنواع الثلاثة يمكن دراستها عند الحلقة المفتوحة Open Loop والحلقة المغلقة Closed Loop. إذا تم الأخذ بعين الاعتبار القيمة المقاسة تسمى الحلقة مغلقة أما إذا تما عزلها فيسمى النمط بالحلقة المفتوحة. سيتم التكيز هنا على PID ذي النوع المتوازي أو المتفرع. تعطى وظيفة الخرج له بالعلاقة:

${\displaystyle \mathrm {MV(t)} =\,P_{\mathrm {out} }+I_{\mathrm {out} }+D_{\mathrm {out} }}$

حيث:

${\displaystyle P_{\mathrm {out} }}$, ${\displaystyle I_{\mathrm {out} }}$, و${\displaystyle D_{\mathrm {out} }}$ هي المساهمات التي تؤديها كل وظيفة من الحدود الثلاثة على حدة إلى الخرج كما سيتبين فيما يلي.

الحد التناسبي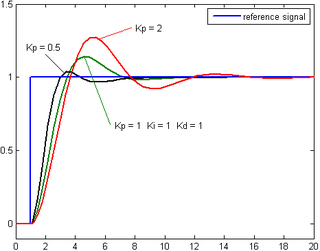

شكل يبين الخرج مقابل الزمن, لقيم مختلفة من K_p (أي أن K_i و K_d تبقى ثابتة) في الحلقة المفتوحة.

شكل يبين PV مقابل الزمن, لقيم مختلفة من K_p (أي أن K_i و K_d تبقى ثابتة) في الحلقة المغلقة.

يدعى أحيانا الحد التناسبي بالتضخيم ويتسبب في تغير قيمة الخرج بمقدار يتناسب طرديا مع قيمة الخطأ الحالية. يمكن ضبط الاستجابة التناسبية بضرب قيمة الخطأ بقيمة ثابتة (قابلة للضبط) K_p, وتدعى أيضا بالتضخيم التناسبي. يستخدم وصفا اخر في بعض أنظمة التحكم هو النطاق التناسبي Proportional Band, ويرمز له عادة PB% ويرتبط بالحد التناسبي بالعلاقة:

${\displaystyle K_{p}={\frac {100}{PB\%}}}$

يكون الخرج الناتج عن الحد التناسبي هو:

${\displaystyle P_{\mathrm {out} }=K_{p}\,{e(t)}}$

حيث: ${\displaystyle P_{\mathrm {out} }\,}$: الحد التناسبي في للخرج: ${\displaystyle K_{p}\,}$: التضخيم التناسبي، قابل للتعديل: ${\displaystyle e\,}$: الخطأ ويساوي ${\displaystyle SP-PV\,}$

${\displaystyle t\,}$: الزمن

إذا كانت قيمة التضخيم التناسبي كبيرة فسينتج عنها تغيرا كبيرا في الخرج عند قيمة معينة للخطأ. أما إذا كانت هذه القيمة كبيرة جدا فسيصبح النظام غير مستقر (انظر قسم موالفة الحلقة في الأسفل).

الجدير بالذكر هو أن الحد التناسبى

لا يستطيع إلغاء الخطأ أو الإزاحة Offset بدون وجود الحد التكاملي. يمكن إثبات ذلك في حالة تغير الخطوة مثلا، باستخدام معادلات لابلاس يمكن إثبات أن الخطأ المتبقي عند زمن الاستقرارية (أي عندما ${\displaystyle t\to \infty \,}$) هو:${\displaystyle e_{ss}=\lim _{t\to \infty }e(t)={\frac {K_{p}}{K_{p}+1}}}$

حيث:

${\displaystyle e_{ss}\,}$ خطأ الحالة المستقرة steady state error (أي عندما ${\displaystyle t\to \infty \,}$).

يستعمل هذا النوع من عناصر التحكم في ضبط الحرارة وبعض التطبيقات الأخرى مثل ضبط مستوى السائل في الخزانات إذا لم تكن عملية إزالة الخطأ ذات أهمية.

الحد التكاملي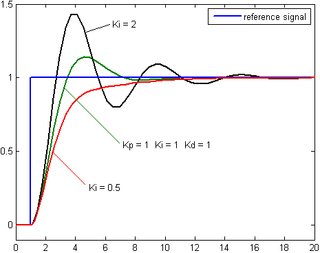

مخطط لقيمة التغير في الخطأ والخرج مع الزمن في الحلقة المفتوحة وذلك لقيم مختلفة من K_i (أي أن K_p وK_d تبقى ثابتة)

مخطط لقيمة PV مع الزمن في الحلقة المغلقة, وذلك لقيم مختلفة من K_i (أي أن K_p وK_d تبقى ثابتة)

يطلق على الحد التكاملي أحيانا إعادة الضبط reset وذلك لقدرته على إزالة الخطأ المتبقي والذي لايستطيع الحد التناسبي إلغاؤه. يمكن فهم السبب بالنظر في الحلقة المفتوحة حيث نرى أن الحد التكاملي يستمر في التغير صعودا أو هبوطا بشكل يتناسب مع مقدار الخطأ مع ولايتوقف مع مرور الوقت إلا إذا كان الخطأ صفرا. عمليا يتوقف الحد التكاملي عندما يصل إلى مرحلة الإشباع وهي القدرة العظمى للخرج العملياتي. يمتلك الحد التكاملي ثابتا قابلا للضبط في عمليات الموالفة ويدعى ${\displaystyle K_{i}\,}$. غالبا يستبدل هذا الثابت بمقلوبه والذي يحمل مغزى للتكامل ويطلق عليه ${\displaystyle T_{i}\,}$ حيث:

${\displaystyle K_{i}={\frac {1}{T_{i}}}\,}$

يعرف Ti على أنه الزمن اللازم للوصول بالخرج لنفس قيمة الخطأ أو الدخل منذ بدء الخطأ بمقدار خطوة Step.

يعطى الحد التكاملي بالعلاقة:

${\displaystyle I_{\mathrm {out} }=K_{i}\int _{0}^{t}{e(\tau )}\,{d\tau }}$

حيث: ${\displaystyle I_{\mathrm {out} }\,}$: الحد التكاملي للخرج: ${\displaystyle K_{i}\,}$: تضخيم التكامل، قابل للموالفة: ${\displaystyle e\,}$: الخطأ ويساوي ${\displaystyle SP-PV\,}$

${\displaystyle t\,}$: الزمن اللحظي.

${\displaystyle \tau \,}$: متغير اعتباطي.

يستعمل الحد التكاملي مع الحد التناسبي بشكل واسع في التطبيقات الصناعية لتعجيل عملية الاستجابة وإزالة الخطأ عند الاستقرارية. ومع ذلك قد يتسبب الحد التكاملي في ظهور نطة overshoot فوق القيمة المراد الوصول لها بسبب تجميعه لبيانات الخطأ المتراكمة. يمكن التوفيق بين سرعة الاستجابة والنطة بواسطة موالفة ثوابت الحدود كما في قسم الموالفة في الأسفل.

الحد التفاضلي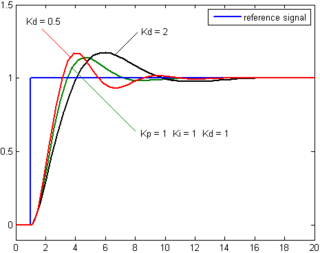

رسم يوضح قيمة PV بالنسبة للزمن, مع ثلاث قيم مختلفة لـ K_d (هنا K_p وK_i تبقى ثابتة)

يطلق على الحد التفاضلي أحيانا بالمعدل rate وذلك لأنه يظهر فقط عندما يكون هناك تغير في قيمة الخطأ بالنسبة للزمن ويتناسب طرديا مع معدل هذا التغير. يمتلك الحد التفاضلي ثابتا قابلا للتغيير في عملية الموالفة ويرمز له رياضيا ${\displaystyle K_{d}\,}$ وفي الأنظمة الصناعية عادة ${\displaystyle T_{d}\,}$ لأنها ترمز لميل دالة الخطأ.

يمكن التعبير عن الحد التفاضلي رياضيا بالصورة:

${\displaystyle D_{\mathrm {out} }=K_{d}{\frac {d}{dt}}e(t)}$

حيث: ${\displaystyle D_{\mathrm {out} }\,}$: الحد التفاضلي للخرج: ${\displaystyle K_{d}\,}$: التضخيم التفاضلي، قابل للموالفة: ${\displaystyle e\,}$: الخطأ ويساوي ${\displaystyle SP-PV\,}$

${\displaystyle t\,}$: الزمن

مع أن الحد التفاضلي يحسن أحيانا في عملية التحكم إلا أنه يتأثر بالضوضاء بشكل كبير ويمكن أن يتسبب في عدم استقرارية النظام. لهذا السبب لايستخدم الحد التفاضلي في الصناعة إلا بشكل نادر وبحذر شديد.

خلاصة

تعمل الحدود التناسبي، التكاملي والتفاضلي معا لتجمع وتعطي خرجا واحدا لعنصر التحكم PID. إذا رمزنا ${\displaystyle u(t)\,}$ لدالة الخرج فستكون قيمتها معطاة بالعلاقة:

${\displaystyle \mathrm {u(t)} =\mathrm {MV(t)} =K_{p}{e(t)}+K_{i}\int _{0}^{t}{e(\tau )}\,{d\tau }+K_{d}{\frac {d}{dt}}e(t)}$

بحيث تكون عناصر الموالفة هي:

التضخيم التناسبي، ${\displaystyle K_{p}}$

ويمكن زيادتها لتسريع الاستجابة ولكن إلى الحد الذي يبقي على استقرارية النظام.

التضخيم التكاملي، ${\displaystyle K_{i}}$

لتسريع عملية إزالة الخطأ.

التضخيم التفاضلي، ${\displaystyle K_{d}}$

لتقليل عملية الطلقة أو النطة مع مراعاة تأثير الضوضاء.

الموالفة

تعد عملية موالفة الحلقة Loop tuning من أعقد وأخطر عمليات التحكم لاسيما الموالفة المباشرة أثناء العمليات والسبب هو عدم وجود قانون ثابت يحكم العملية Process. إذا أخطأنا باختيار القيم المناسبة لعناصر الموالفة (معاملات المضخم التناسبي، التكاملي، والتفاضلي) يمكن أن تصبح العملية المراد التحكم بها غير مستقرة وربما تخرج عن السيطرة. فبدلا عن الحصول على قيمة مستقرة بعد فترة من الزمن قد يصبح هناك إما وقت أطول للحصول على هذه القيمة المستقرة أو ربما لا تستقر وتظل في حالة تذبذب طوال الوقت وربما ما هو أسوأ وهو تضخيم عملية التذبذب مع الوقت حتى تخرج عن السيطرة تماما.

هناك بعض الطرق المشهورة في عملية الموالفة التقريبية والتي تحاول الاستفادة من تجربة عملية (تتم عادة بالأسلوب اليدوي Manual Mode) أولية أو أكثر على العملية Process وقد تكون إما حلقة مفتوحة أو مغلقة أشهرها مايلي.

اختيار طريقة الموالفة
الطريقة	المزايا	العيوب
الموالفة اليدوية	لا تحتاج لحسابات رياضية. تتم مياشرة أثناء سيران العمليات.	تتطلب أفراد ذوي خبرة.
Ziegler–Nichols زيغلر-نيكولس	طريقة مثبتة. مباشرة أثناء سيران العمليات online.	اضطراب في العمليات، تعتمد على التجربة والخطأ، موالفة تتطلب المزيد من الكفاح.
Software Toolsأدوات برامجية	موالفة متسقة. طريقة مباشرة أو حتى أثناء توقف العمليات. قدد تتضمن معها عملية تحليل للمحبس والمجس. السماح بالمحاكاة قبل التنزيل.	تتطلب دورة تدريبية مكلفة.
Cohen-Coonكوهن-كون	نماذج جيدة للعمليات.	بعض الرياضيات. أثناء توقف العمليات. مناسبة فقط لعمليات من الرتبة الأولى.

الموالفة اليدوية

عندما يكون من الضروري بقاء النظام عاملا، يمكن أولا موالفة ${\displaystyle K_{i}}$ و${\displaystyle K_{d}}$ إلى قيم صفرية. يتم زيادة ${\displaystyle K_{p}}$ تدريجيا حتى يبدأ خرج الحلقة بالتذبذب، حينئذ ينبغي إنقاص قيمة ${\displaystyle K_{p}}$ إلى النصف تقريبا من أجل استجابة من نوع «اضمحلال ربع الاتساع». ثم تزاد قيمة ${\displaystyle K_{i}}$ حتى يتم تصحيح أي انزياح خلال زمن كاف للعملية. ومع ذلك، فإن زيادة كبيرة جدا في ${\displaystyle K_{i}}$ ستسبب عدم استقرارية. وأخيرا، يتم زيادة${\displaystyle K_{d}}$, إذا كان مطلوبا، حتى تصبح الحلقة سريعة بشكل ماقبل وبعد حدوث اضطراب في حمل. ولكن مرة أخرى، فإن زيادة ${\displaystyle K_{d}}$ كثيرا قد يتسبب في استجابة زائدة عن الحاجة وظهور النطة. في العادة تتسبب عملية الموالفة السريعة في PID بظهور نطة طفيفية من أجل الوصول لقيمة الضبط setpoint بشكل أسرع; بالرغم من هذا، فبعض الأنظمة لا تتقبل هذه النطة، وفي هذه الحال يكون النظام المغلق ذو «إخماد قوي over-damped» ضروريا، والذي يتطلب ضبط ${\displaystyle K_{p}}$ أقل من نصف القيمة ${\displaystyle K_{p}}$ التي تسببت في التذبذب.

تأثيرات زيادة المعاملات
المعامل	زمن الصعود	النطة	زمن الاستقرار	الخطأ عند الاتزان
${\displaystyle K_{p}}$	نقص	زيادة	تغير طفيف	نقص
${\displaystyle K_{i}}$	نقص	زيادة	زيادة	عزل
${\displaystyle K_{d}}$	لانهائي (نقص أو زيادة طفيفة)[1]	نقص	نقص	لاشيئ

طريقة زيغلر نيكولس

سميت هذه الطريقة نسبة لمقدميها جون زيغلر وناتانيل نيكولس. كما الطريقة السابقة، توضع قيم ${\displaystyle K_{i}}$ و${\displaystyle K_{d}}$ على الصفر. تزاد قيمة التضخم P حتى تصل إلى التضخيم الحرج، ${\displaystyle K_{c}}$, حيث يبدأ الخرج بالتذبذب. ${\displaystyle K_{c}}$ وفترة التذبذب ${\displaystyle P_{c}}$ تستعمل لضبط القيم كما يلي:

طريقة زيغلر نيكولس
نوع التحكم	${\displaystyle K_{p}}$	${\displaystyle K_{i}}$	${\displaystyle K_{d}}$
P	${\displaystyle 0.50{K_{c}}}$	-	-
PI	${\displaystyle 0.45{K_{c}}}$	${\displaystyle 1.2{K_{p}}/P_{c}}$	-
PID	${\displaystyle 0.60{K_{c}}}$	${\displaystyle 2{K_{p}}/P_{c}}$	${\displaystyle {K_{p}}{P_{c}}/8}$

برامج موالفة PID

لم تعد الطرق التقليدية السابقة مستخدمة كثيرا في أنظمة التحكم الصناعية الحديثة. بدلا من ذلك تقوم برامج حديثة بعمل الموالفة والأمثلية. تقوم هذه البرامج بجمع البيانات، تطوير نماذج عمليات، ومن ثم تقترح الموالفة المثلى كما أن بعض هذه البرامج تستطيع تطوير عملية الموالفة بالاعتماد على تغييرات مرجعية (كما في أنظمة APC التحكم المتقدم بالعمليات).

تكمن فكرة موالفة الحلقة الرياضية في استحثاث قدحة Impulse في النظام، ثم تسخير الاستجابة الترددية للنظام المحكوم لتصميم قيم حلقة PID المطلوبة. تفضل هذه العملية في حالة الحلقات التي تتراوح استجابتها الزمنية بضع دقائق. من الصعوبة بمكان إيجاد القيم المثلى. تقدم بعض حلقات التحكم الرقمية ميزة «الموالفة الذاتية» حيث يتم إرسال تغيرات طفيفة جدا في القيمة المضبوطة SP إلى العمليات، سامحة لأجهزة التحكم بحساب قيم موالفة مثلى.

البرمجة

يمكن برمجة عناصر التحكم السابقة في حلقة مغلقة افتراضية دون الحاجة لتصنيعها عمليا وهذا هو فعلا ماتقوم به أنظمة التحكم الحديث. المثال التالي يمثل كيفية بناء البرنامج باستعمال لغة كيو بيسك مثلا:

 previous_error = 0
 integral = 0 
 begin:
   recent_error = setpoint - actual_position
   integral = integral + (recent_error*dt)
   derivative = (recent_error- previous_error)/dt
   recent_output = (Kp*recent_error) + (Ki*integral) + (Kd*derivative)
   previous_error = recent_error
   SLEEP (dt)
   GOTO begin

المصادر

1. https://web.archive.org/web/20181005021517/http://saba.kntu.ac.ir/eecd/pcl/download/PIDtutorial.pdf. مؤرشف من الأصل (PDF) في 2018-10-05. {{استشهاد ويب}}: الوسيط |title= غير موجود أو فارغ (مساعدة)