|
جوامع منطقيةالجامع المنطقي (بالإنجليزية: Adder) هو عبارة عن دائرة ألكترونية رقمية تقوم بوظيفة جمع الأرقام.[1] يستخدم الجامع المنطقي في وحدة الحساب والمنطق في المعالجات الدقيقة وغيرها من أنواع المعالجات الأخرى، ولكن لا يقتصر استخدام الجامع في وحدة الحساب والمنطق ولكنه يتمتد إلى أجزاء أخرى من المعالج حيث يقوم الجامع المنطقي بحساب العنواين وفهارس الجداول ومشغلات الزيادة والنقص وغيرها من العمليات المشابهة. علي الرغم من أن الجامع المنطقي يمكن بناؤه ليتوافق مع العديد من نُظم التمثيلات الرقمية كنطام التمثيل العشري المشفر ثنائيا أو نظام إكسيس-3 إلا أن أكثر نظام رقمي يتم استخدام الجامع فيه هو نظام الأعداد الثنائية. حيث في حالة استخدام متمم ثنائي أو متمم أحادي يمكن يتم تعديل الجامع المنطقي ليصبح جامع طارح، ميزة أخرى لاستخدام المتمم الثنائي أو الأحادي هو عدم الحاجة لدوائر إضافية للتعامل مع الإشارة (سالب وموجب) حيث يتطلب ترميز الأعداد الصحيحة بإشارة [الإنجليزية] الأخرى إضافة دوائر منطقية إضافية بجانب الجامع للتعامل مع الإشارة. نصف الجامع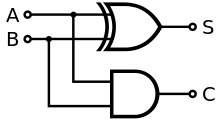 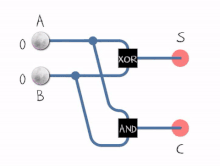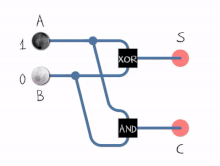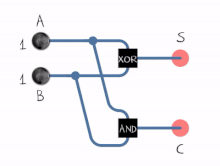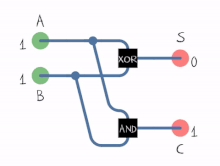 نصف الجامع[2] (بالإنجليزية: Half Adder) عبارة عن دائرة إلكترونية مؤلفة من بوابات منطقية تقوم بجمع رقمين ثنائيين مكون كل منهما من بت واحد. ولهذه الدائرة مدخلان ومخرجان فقط يوضع الرقمان المراد جمعهما على المداخل أما المخارج فالأول يمثل نتيجة الخرج والثانى يمثل الحمل (الفيض) carry ويبين الشكل التالي دائرة الجامع النصفي: ويمكن توضيح عمل نصف الجامع من خلال الجدول المنطقي التالي:
من خلال هذا الجدول يمكن تمثيل معادلات النتيجة والفيض كدوال بالنسبة للمدخلات A، B فلو أخذنا الدالة S فإن قيمتها تكون مساوية للواحد في حالتين: 1- عندما تكون A=0 وB=1 وبهذا تؤلف هذه القيم الحد الأول AB 2- عندما تكون A=1 وB=0 وتؤلف هذه القيم الحد الثاني AB وبهذا تصبح S كما يلي: S= A.Bَ + Aَ.B أما بالنسبة لمعادلة الفيض فإنها تحتوي على حد واحد (لاحظ قيمة C تكون مساوية للواحد في حالة واحد وهي عندما تكون A=1 وB=1) وبهذا فإن C تصبح كما يلي: C=A.B الجامع الكامليعرف الجامع الكامل (بالإنجليزية: Full Adder) على أنه دائرة إلكترونية لها ثلاثة مداخل ومخرجان حيث يستخدم لجمع ثلاثة أرقام كل منها مؤلف من خانة واحدة بت ويمثل الجامع الكامل حسب الشكل التالي: ويمكن فهم عمل هذا الجامع من خلال الجدول المنطقي التالي: من خلال هذا الجدول يمكن استنتاج معادلة C، S ومن خلال هذه المعادلات يمكن بناء دارة الجامع الكامل والتي تأخذ الشكل التالي: ولو فرضنا A, B, CI المداخل، فنحصل على المجموع si ونرمز له ∑ كما في الدارة التالية: ونحصل على الحمل Ci الذي نرمز له Co كما في الدارة التالية: ويوجد أنواع للجامع الكامل ومنه: جامع الحمل المنتشر: Ripple-carry adderجامع التتبع بالحمل: Carry-lookahead adderإن قيمة C1(الحمل الثاني)لاتنتظر قيمة C0(الحمل الأول)وأيضاً C2(الحمل الثالث)لاتنتظر قيمة C0 وC1 نكسب في هذه الدارة زمن أي لايوجد زمن في انتقال الحمل من خانة لأخرى ولكن يصبح عدد البوابات أكثر. وهي داره غير فعاله لكثره عدد البوابات المصادر
انظر ايضاً |
||||||||||||||||||||||||