بيان مستو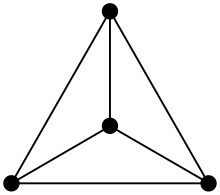

رسم يوضح المخطط المستوي المكون من أربع حلقات.

في المخططات، المخطّط المستوي هو المخطّط الذي يقبل تمثيلا في المستوى، بحيث لا يتقاطع أي حرفين من المخطّط.[1][2][3]

معايير المخطّط المستوي

حسب كوراتوفسكي, يكون المخطط مستويا إذا لم يتضمن زمرة من الرتبة الخامسة، أو مخططا ثنائيا كاملا من الرتبة الثالثة.

وجوه مخطط مستوي

ليكن G مخططا مستويا، الوجه F هو أكبر منطقة من المستوى محدّدة بمجموعة حروف G ولا تتضمن أيا منها.

ليكن G مخطّطا مستويا، و a عدد حروف G. إذن : ${\displaystyle \sum _{F}^{}deg(F)=2a}$

صيغة أويلر

تعاريف

• المسار ذو الطول r هو سلسلة ${\displaystyle (S_{0},...,S_{r})}$ من القمم المرتبطة مع ${\displaystyle S_{0}}$ أصل السبيل و${\displaystyle S_{r}}$ طرفه.
• يكون المخطّط متّصلا إذا وُجد مسار بين كل قمتين من G.
• المسار المغلق هو حالة ${\displaystyle S_{0}=S_{r}}$.
• الشجرة هي مخطط متّصل بدون أي مسار مغلق.

تمهيدة

كل مخطّط متّصل يمكن الحصول عليه بإضافة عدّة قمم لشجرة (لها نفس عدد القمم).

صيغة أويلر للمخطّطات المستوية المتّصلة

ليكن G مخطّط مستوي متّصل. ليكن n عدد قمم a, G عدد حروفه و f عدد وجوهه. إذن: n − a + f = 2

المعايير

تحديد المعايير التي تمكّن من معرفة ان كان مخطّط ما مستويا. ليكن G مخطّط مستوي متّصل. ليكن n عدد قمم a, G عدد حروفه:

1. ${\displaystyle a\leq {3n-6}}$ في حالة وجود مثلّثات.
2. ${\displaystyle a\leq {2n-4}}$ في حالة عدم وجود مثلّثات.

مميّزة كوراتوفسكي

الرياضي البولوني كوراتوفسكي وضع الميّزة التالية للمخطّطات المستوية :

يكون المخطّط مستويا إذا وفقط إذا لم يتضمّن مخطّطا جزئيّا عبارة عن تمديد ل K₅ (زمرة ب 5 قمم) أو K_3,3 (المخطّط ثنائي كامل ب3+3 رؤوس).

'التمديد بالنّسبة لمخطّط هو نتيجة إضافة قـمّة أو أكثر لحرف أو عدّة حروف (مثلا، تحويل الحرف•——• إلى •—•—•).

انظر أيضًا

• مخطط مزدوج
• نظرية المخططات

مراجع

1. Trudeau، Richard J. (1993). Introduction to Graph Theory (ط. Corrected, enlarged republication.). New York: Dover Pub. ص. 64. ISBN:978-0-486-67870-2. مؤرشف من الأصل في 2019-05-05. اطلع عليه بتاريخ 2012-08-08. Thus a planar graph, when drawn on a flat surface, either has no edge-crossings or can be redrawn without them.
2. Bonichon، N.؛ Gavoille، C.؛ Hanusse، N.؛ Poulalhon، D.؛ Schaeffer، G. (2006). "Planar Graphs, via Well-Orderly Maps and Trees". Graphs and Combinatorics. ج. 22: 185–202. CiteSeerX:10.1.1.106.7456. DOI:10.1007/s00373-006-0647-2.
3. Giménez، Omer؛ Noy، Marc (2009). "Asymptotic enumeration and limit laws of planar graphs". Journal of the American Mathematical Society. ج. 22: 309–329. arXiv:math/0501269. DOI:10.1090/s0894-0347-08-00624-3.