|
Diameter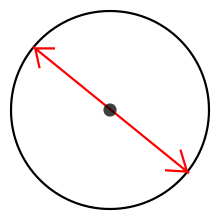  Diameter (dari bahasa Yunani, diairo = bagi dan metro = ukuran) sebuah lingkaran, dalam geometri, adalah segmen garis lurus yang melintasi titik pusat dan menghubungkan dua titik pada lingkaran tersebut, atau, dalam penggunaan modern, diameter berarti panjang dari segmen garis tersebut. Dalam sebuah bola, diameter menghubungkan 2 titik pada permukaan bola dan melalui titik pusat bola. Dalam bahasa Indonesia juga disebut "garis tengah" atau "garis pusat". MatematikaDiameter merupakan tali busur terpanjang pada suatu lingkaran. Semua diameter d dalam suatu lingkaran atau bola mempunyai panjang yang sama, yaitu dua kali jari-jari r. Dalam suatu bentuk konveks dalam sebuah bidang datar (plane), "diameter" didefinisikan sebagai jarak terjauh dari dua tangen garis sejajar yang terletak berlawanan pada batas-batasnya, dan "lebar" (width) didefinisikan sebagai jarak terpendek. Kedua kuantitas dapat dihitung secara efisien dengan menggunakan jangka berputar.[1] Diameter dapat digunakan untuk mengetahui keliling dan luas lingkaran. Dalam bola 3 dimensi, diameter dapat digunakan untuk mengetahui luas permukaan dan volume bola. Simbol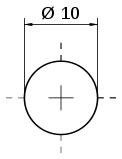 Simbol (lambang) atau variabel untuk diameter, ⌀, mirip dalam ukuran dan desain dengan ø, huruf kecil abjad Latin o dengan garis miring. Dalam Unicode didefinisikan sebagai U+2300 ⌀ diameter sign (HTML: Simbol diameter ⌀ berbeda dengan simbol "himpunan kosong" ∅, yang berasal dari (italik) huruf besar Fi Φ, dan dari huruf hidup Nordik Ø.[2] Lihat pulaLihat entri diameter di kamus bebas Wiktionary.
Referensi
|
